题目内容
若sinx=sin(
-x)=
,则tanx+tan(
-x)的值是( )
| 3π |
| 2 |
| 2 |
| 3π |
| 2 |
| A、-2 | B、-1 | C、1 | D、2 |
分析:把已知的三角等式利用诱导公式变形求解tanx,把要求值的三角函数式也转化成tanx,代入正切值后即可得到答案.
解答:解:由sinx=sin(
-x),得:sinx=sin[π+(
-x)]=-sin(
-x)=-cosx.
显然cosx≠0,∴
=-1,即tanx=-1.
tanx+tan(
-x)=tanx+tan[π+(
-x)]=tanx+tan(
-x)
=tanx+cotx=tanx+
=
=
=-2.
故选A.
| 3π |
| 2 |
| π |
| 2 |
| π |
| 2 |
显然cosx≠0,∴
| sinx |
| cosx |
tanx+tan(
| 3π |
| 2 |
| π |
| 2 |
| π |
| 2 |
=tanx+cotx=tanx+
| 1 |
| tanx |
| tan2x+1 |
| tanx |
| (-1)2+1 |
| -1 |
故选A.
点评:本题考查了运用三角函数的诱导公式化简求值,考查了同角三角函数间的基本关系,属中档题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
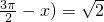 ,则tanx+tan(
,则tanx+tan(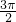 -x)的值是
-x)的值是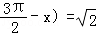 ,则tanx+tan(
,则tanx+tan(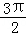 ﹣x)的值是
﹣x)的值是