题目内容
 已知椭圆的中心在原点,焦点在x轴上,离心率为
已知椭圆的中心在原点,焦点在x轴上,离心率为
| ||
| 2 |
(Ⅰ)求椭圆的方程;
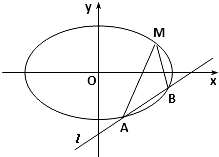
(Ⅱ)若直线l不过点M,求证:直线MA,MB与x轴围成等腰三角形.
分析:(Ⅰ)设出椭圆方程的标准形式,由离心率的值及椭圆过点(4,1)求出待定系数,得到椭圆的标准方程.
(Ⅱ)把直线方程代入椭圆的方程,由判别式大于0,求出m的范围,可得到两根之和、两根之积,设直线MA,MB斜率分别为k1和k2,化简k1+k2 的结果等于0,即说明MB与x轴所围的三角形为等腰三角形.
(Ⅱ)把直线方程代入椭圆的方程,由判别式大于0,求出m的范围,可得到两根之和、两根之积,设直线MA,MB斜率分别为k1和k2,化简k1+k2 的结果等于0,即说明MB与x轴所围的三角形为等腰三角形.
解答:解:(1)设椭圆方程为
+
=1,因为e=
,所以a2=4b2,又椭圆过点M(4,1),所以
+
=1,解得b2=5,a2=20,故椭圆方程为
+
=1(5分)
(2)将y=x+m代入
+
=1并整理得5x2+8mx+4m2-20=0,△=(8m)2-20(4m2-20)>0得:5>m>-5.
设直线MA,MB斜率分别为k1和k2,只要证k1+k2=0,
设A(x1,y1),B(x2,y2),则x1+x2 =-
,x1x2=
k1+k2=
+
=
分子=(x1+m-1)(x2-4)+(x2+m-1)(x1-4)
=2x1x2+(m-5)(x1+x2)-8(m-1)
-
-8(m-1)=0
因此MA,MB与x轴所围的三角形为等腰三角形.(14分)
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 16 |
| a2 |
| 1 |
| b2 |
| x2 |
| 20 |
| y2 |
| 5 |
(2)将y=x+m代入
| x2 |
| 20 |
| y2 |
| 5 |
设直线MA,MB斜率分别为k1和k2,只要证k1+k2=0,
设A(x1,y1),B(x2,y2),则x1+x2 =-
| 8m |
| 5 |
| 4m-20 |
| 5 |
k1+k2=
| y1-1 |
| x1-4 |
| y2-1 |
| x2-4 |
| (y1-1)(x2-4)+(y2-1)(x1-4) |
| (x1-4)(x2-4) |
分子=(x1+m-1)(x2-4)+(x2+m-1)(x1-4)
=2x1x2+(m-5)(x1+x2)-8(m-1)
| 2(4m2-20) |
| 5 |
| 8m(m-5) |
| 5 |
因此MA,MB与x轴所围的三角形为等腰三角形.(14分)
点评:本题考查用待定系数法求椭圆的标准方程,一元二次方程根与系数的关系,体现了等价转化的数学思想.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目