题目内容
19．已知D、E、F分别是△ABC的中点，写出以A、B、C、D、E、F这六点中任意两个点为起点和终点的向量中与$\overrightarrow{AB}$平行的所有向量．分析 结合图形，利用列举法求解．
解答 解：如图所示，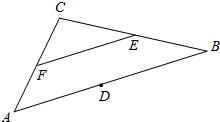
根据三角形中位线定理，可得FE∥AB，
∴与$\overrightarrow{AB}$平行的所有向量为$\overrightarrow{FE}$，$\overrightarrow{EF}$，$\overrightarrow{AD}$，$\overrightarrow{DA}$，$\overrightarrow{DB}$，$\overrightarrow{BD}$，$\overrightarrow{BA}$，
点评 本题考查平行向量的个数的求法，是基础题，解题时要认真审题，注意数形结合思想的合理运用．
练习册系列答案
相关题目
14．定义在[-1，1]上的偶函数y=f（x）满足：对于任意的x1，x2∈[0，1]（x1≠x2），都有（x2-x1）（f（x2）-f（x1））＞0，则满足f（2x-1）≤f（2x）的x的取值范围是（ ）
| A． | [$\frac{1}{4}$，$\frac{1}{2}$] | B． | [$\frac{1}{4}$，1] | C． | [0，1] | D． | [0，$\frac{1}{2}$] |
4．若k∈R，则直线（k+2）x+（1-k）y-3=0必通过点（ ）
| A． | （-1，-1） | B． | （1，1） | C． | （-1，-2） | D． | （1，2） |
8．函数f（x）=x-x3为 （ ）
| A． | 奇函数 | B． | 偶函数 | ||
| C． | 既是奇函数又是偶函数 | D． | 既不是奇函数又不是偶函数 |