题目内容
(9分)已知函数 .
.
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)当 时,函数
时,函数 的图象与x轴围成草垛型平面区域,为了估算该区域的面积,采用计算机随机模拟试验,先产生0~2之间的均匀随机数A, 0~1之间的
的图象与x轴围成草垛型平面区域,为了估算该区域的面积,采用计算机随机模拟试验,先产生0~2之间的均匀随机数A, 0~1之间的 均匀随机数B,再判断
均匀随机数B,再判断 是否成立. 我们做2000次试验,得到1273次
是否成立. 我们做2000次试验,得到1273次 ,由此试估算该草垛型平面区域的面积(结果保留两位小数).
,由此试估算该草垛型平面区域的面积(结果保留两位小数).

 .
.(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)当
 时,函数
时,函数 的图象与x轴围成草垛型平面区域,为了估算该区域的面积,采用计算机随机模拟试验,先产生0~2之间的均匀随机数A, 0~1之间的
的图象与x轴围成草垛型平面区域,为了估算该区域的面积,采用计算机随机模拟试验,先产生0~2之间的均匀随机数A, 0~1之间的 均匀随机数B,再判断
均匀随机数B,再判断 是否成立. 我们做2000次试验,得到1273次
是否成立. 我们做2000次试验,得到1273次 ,由此试估算该草垛型平面区域的面积(结果保留两位小数).
,由此试估算该草垛型平面区域的面积(结果保留两位小数).
(1)略
(2)得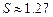 .
.
(2)得
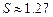 .
.解:(1)先列表,后描点并画图
………(3分)
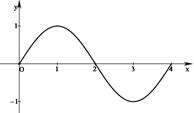 ……(5分)
……(5分)
(2)A为0~2之间的均匀随机数, B为0~1之 间的均匀随机数,点
间的均匀随机数,点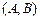 所落区域为
所落区域为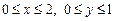 的矩形内,面积为
的矩形内,面积为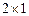 . 如果
. 如果 ,则点
,则点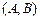 即落草垛型平面区域内. 设草垛型区域面积为S,则
即落草垛型平面区域内. 设草垛型区域面积为S,则
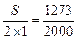 ,解得
,解得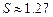 . ……(9分)
. ……(9分)
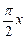 | 0 | 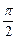 | π | 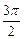 | 2π |
| x | 0 | 1 | 2 | 3 | 4 |
| y | 0 | 1 | 0 | -1 | 0 |
 ……(5分)
……(5分)(2)A为0~2之间的均匀随机数, B为0~1之
 间的均匀随机数,点
间的均匀随机数,点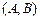 所落区域为
所落区域为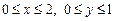 的矩形内,面积为
的矩形内,面积为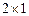 . 如果
. 如果 ,则点
,则点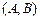 即落草垛型平面区域内. 设草垛型区域面积为S,则
即落草垛型平面区域内. 设草垛型区域面积为S,则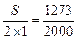 ,解得
,解得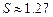 . ……(9分)
. ……(9分)
练习册系列答案
相关题目
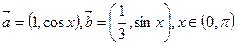
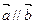 ,求
,求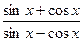 的值;
的值;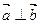 ,求
,求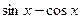 的值。
的值。 ,sin
,sin ,求角
,求角 求
求 的值.
的值.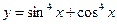 的单调递增区间是___________________
的单调递增区间是___________________ =
= 、Sin
、Sin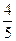 ,则角
,则角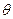 的终边落在直线( )上。
的终边落在直线( )上。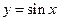 和
和 的图象在
的图象在 内的所有交点中,能确定的不同直线的条数是 ( )
内的所有交点中,能确定的不同直线的条数是 ( )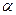 的顶点在原点,始边与
的顶点在原点,始边与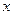 轴非负半轴重合,终边为射线
轴非负半轴重合,终边为射线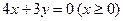 ,则
,则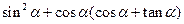 的值是
的值是
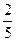
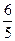
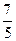
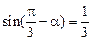 ,则
,则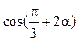 =_________.
=_________.