题目内容
若函数 是R是的单调递减函数,则实数
是R是的单调递减函数,则实数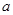 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
B
解析试题分析:由题意,此分段函数是一个减函数,故一次函数系数为负,且在分段点处,函数值应是右侧小于等于左侧,由此得相关不等式,即可求解。依题意可知a-2<0, ,故答案为B
,故答案为B
考点:本题主要考查分段函数单调性的运用。
点评:解决该试题的关键是利用分段函数在整个实数域上递减,则说明要满足的条件有:每一段函数都是递减的,同时要注意断点处的函数值,左边的函数值要大于等于右边的函数值。熟知一些基本函数的单调性是正确解对本题的关键,本题中有一易错点,忘记验证分段点出函数值的大小验证,做题时要注意考虑完全.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
方程 的实数解落在的区间是
的实数解落在的区间是
A. | B. | C. | D. |
已知定义在R上的奇函数
 ,满足
,满足 ,且在区间[0,2]上是增函数,则( )
,且在区间[0,2]上是增函数,则( )
A. | B. |
C. | D. |
设偶函数 的定义域为R,当
的定义域为R,当
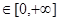 时,
时, 是增函数,则
是增函数,则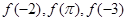 的大小关系是( )
的大小关系是( )
A. | B. |
C. | D. |
已知二次函数 的导数为
的导数为 ,
, ,对于任意实数
,对于任意实数 ,有
,有 ,则
,则 的最小值为
的最小值为
A.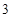 | B. | C. | D. |
下列两个函数完全相同的是( )
A. 与 与 | B. 与 与 |
C. 与 与 | D. 与 与 |
函数 的定义域是( )
的定义域是( )
A.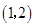 | B.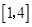 | C. | D. |
已知函数 有2个不同的零点
有2个不同的零点 、
、 ,则
,则
A. | B.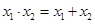 |
C. | D. |
 与
与 的图象是 ( )
的图象是 ( )