题目内容
3.A、B、C三点在同一球面上,∠BAC=135°,BC=2,且球心O到平面ABC的距离为1,则此球O的体积为4$\sqrt{3}π$.分析 运用正弦定理可得△ABC的外接圆的直径2r,再由球的半径和球心到截面的距离、及截面圆的半径构成直角三角形,即可求得球的半径,再由球的体积公式计算即可得到.
解答 解:由于∠BAC=135°,BC=2,
则△ABC的外接圆的直径2r=$\frac{2}{sin135°}$=2$\sqrt{2}$,
即有r=$\sqrt{2}$,
由于球心O到平面ABC的距离为1,
则由勾股定理可得,球的半径R=$\sqrt{{r}^{2}+{d}^{2}}$=$\sqrt{2+1}$=$\sqrt{3}$,
即有此球O的体积为V=$\frac{4}{3}$πR3=$\frac{4}{3}$π×($\sqrt{3}$)3=4$\sqrt{3}π$.
故答案为:4$\sqrt{3}π$.
点评 本题考查球的体积的求法,主要考查球的截面的性质:球的半径和球心到截面的距离、及截面圆的半径构成直角三角形,同时考查正弦定理的运用:求三角形的外接圆的直径,属于中档题.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
14.若(2x+$\frac{1}{\root{3}{x}}$)n的展开式中所有项的二项式系数之和为64,则该二项式的展开式中x2项的系数为( )
| A. | 180 | B. | 160 | C. | 120 | D. | 80 |
15.正三角形ABC的边长为2,将它沿高AD翻折,使点B与点C间的距离为$\sqrt{3}$,此时四面体ABCD外接球表面积为( )
| A. | 7π | B. | 19π | C. | $\frac{7}{6}$$\sqrt{7}$π | D. | $\frac{19}{6}$$\sqrt{19}$π |
11.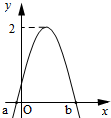 如图是函数$f(x)=Asin(2x+φ)(|φ|≤\frac{π}{2})$图象的一部分,对不同的x1,x2∈[a,b],若 f(x1)=f(x2),有$f({x_1}+{x_2})=\sqrt{3}$,则( )
如图是函数$f(x)=Asin(2x+φ)(|φ|≤\frac{π}{2})$图象的一部分,对不同的x1,x2∈[a,b],若 f(x1)=f(x2),有$f({x_1}+{x_2})=\sqrt{3}$,则( )
 如图是函数$f(x)=Asin(2x+φ)(|φ|≤\frac{π}{2})$图象的一部分,对不同的x1,x2∈[a,b],若 f(x1)=f(x2),有$f({x_1}+{x_2})=\sqrt{3}$,则( )
如图是函数$f(x)=Asin(2x+φ)(|φ|≤\frac{π}{2})$图象的一部分,对不同的x1,x2∈[a,b],若 f(x1)=f(x2),有$f({x_1}+{x_2})=\sqrt{3}$,则( )| A. | f(x)在$(-\frac{5π}{12},\frac{π}{12})$上是减函数 | B. | f(x)在$(\frac{π}{3},\frac{5π}{6})$上是减函数 | ||
| C. | f(x)在$(-\frac{5π}{12},\frac{π}{12})$上是增函数 | D. | f(x)在$(\frac{π}{3},\frac{5π}{6})$上是减函数 |
18.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(b>a>0)的两条渐近线的夹角为60°,则双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{4}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
8.三个实数a、b、c成等比数列,若a+b+c=l成立,则b的取值范围是( )
| A. | (0,$\frac{1}{3}$] | B. | [-1,$\frac{1}{3}$] | C. | [-$\frac{1}{3}$,0) | D. | [-1,0)∪(0,$\frac{1}{3}$] |
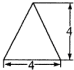 一个四棱锥的底面是正方形,其正视图和侧视图均为如图所示的等腰三角形,则该四棱锥的侧面积为16$\sqrt{5}$.
一个四棱锥的底面是正方形,其正视图和侧视图均为如图所示的等腰三角形,则该四棱锥的侧面积为16$\sqrt{5}$.