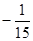题目内容
函数f(x)=ax2+ax-1在R上恒满足f(x)<0,则a的取值范围是( )
| A.a≤0 | B.a<-4 |
| C.-4<a<0 | D.-4<a≤0 |
D
解析

练习册系列答案
相关题目
若不等式 对任意的
对任意的 上恒成立,则
上恒成立,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
(5分)(2011•广东)设f(x),g(x),h(x)是R上的任意实值函数,如下定义两个函数(f°g)(x)和((f•g)(x)对任意x∈R,(f°g)(x)=f(g(x));(f•g)(x)=f(x)g(x),则下列等式恒成立的是( )
| A.((f°g)•h)(x)=((f•h)°(g•h))(x) |
| B.((f•g)°h)(x)=((f°h)•(g°h))(x) |
| C.((f°g)°h)(x)=((f°h)°(g°h))(x) |
| D.((f•g)•h)(x)=((f•h)•(g•h))(x) |
已知函数 与
与 图象上存在关于
图象上存在关于 轴对称的点,则
轴对称的点,则 的取值范围是( )
的取值范围是( )
A. | B. | C.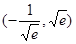 | D. |
已知函数 ,若
,若 互不相等,且
互不相等,且 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
 的图象向左平移1个单位,再将位于
的图象向左平移1个单位,再将位于 轴下方的图象沿
轴下方的图象沿 的图象,若实数
的图象,若实数 满足
满足
 则
则 的值是( )
的值是( )