题目内容
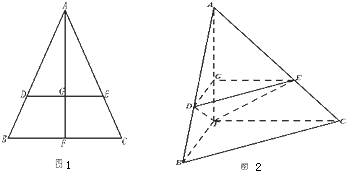 如图1,在边长为3的等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF沿AF折起,得到如图2所示的三棱锥A-BCF,其中BC=
如图1,在边长为3的等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF沿AF折起,得到如图2所示的三棱锥A-BCF,其中BC=3
| ||
| 2 |
(1)证明:DE∥平面BCF;
(2)证明:CF⊥平面ABF;
(3)当AD=
| 2 |
| 3 |
分析:(1)根据面面平行的性质定理证DE∥平面BCF.
(2)利用线面垂直的判定定理证明CF⊥平面ABF.
(3)根据三棱锥的体积公式求体积即可.
(2)利用线面垂直的判定定理证明CF⊥平面ABF.
(3)根据三棱锥的体积公式求体积即可.
解答:解:(1)在等边三角形ABC中,AD=AE,
∴DE∥BC,DG∥BC,GE∥FC
在折叠后的三棱锥A-BCF中也成立,
∵DG∩GE=G,
∴面DGE∥面BFC,又DE?面DGE,
∴DE∥平面BCF.
(2)在等边三角形ABC中,F是BC的中点,
∴AF⊥BC,即AF⊥CF ①,
在边长为3的等边三角形ABC中,BF=FC=
.
∵在三棱锥A-BCF中,BC=
,
∴BC2=BF2+CF2,∴CF⊥BF②.
又∵BF∩AF=F,
∴CF⊥平面ABF.
(3)由(1)可知GE∥CF,结合(2)可得GE⊥平面DFG.
∴三角形EGD为等腰直角三角形.
∵AD=
,
∴DG=GE=
AD=
×
=
.
∵AF=
,AG=
,
∴GF=AF-AG=
-
=
.
∴三棱锥F-DEG的体积VF-DEG=
×
×
×
×
=
.
∴DE∥BC,DG∥BC,GE∥FC
在折叠后的三棱锥A-BCF中也成立,
∵DG∩GE=G,
∴面DGE∥面BFC,又DE?面DGE,
∴DE∥平面BCF.
(2)在等边三角形ABC中,F是BC的中点,
∴AF⊥BC,即AF⊥CF ①,
在边长为3的等边三角形ABC中,BF=FC=
| 3 |
| 2 |
∵在三棱锥A-BCF中,BC=
3
| ||
| 2 |
∴BC2=BF2+CF2,∴CF⊥BF②.
又∵BF∩AF=F,
∴CF⊥平面ABF.
(3)由(1)可知GE∥CF,结合(2)可得GE⊥平面DFG.
∴三角形EGD为等腰直角三角形.
∵AD=
| 2 |
| 3 |
∴DG=GE=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
∵AF=
3
| ||
| 2 |
| ||
| 3 |
∴GF=AF-AG=
3
| ||
| 2 |
| ||
| 3 |
7
| ||
| 6 |
∴三棱锥F-DEG的体积VF-DEG=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
7
| ||
| 6 |
7
| ||
| 324 |
点评:本题主要考查了空间直线和平面平行,以及直线和平面垂直的判定,以及空间几何体的体积的计算,要求熟练掌握相应的判定定理,以及体积公式,考查学生的运算能力.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
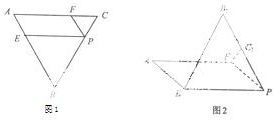 如图1,在边长为3的正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE=CF=CP=1,今将△BEP、△CFP分别沿EP、FP向上折起,使边BP与边CP所在的直线重合(如图2),B、C折后的对应点分别记为B、C1.
如图1,在边长为3的正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE=CF=CP=1,今将△BEP、△CFP分别沿EP、FP向上折起,使边BP与边CP所在的直线重合(如图2),B、C折后的对应点分别记为B、C1.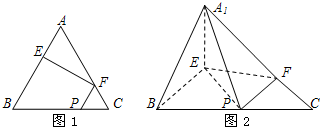 如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,
如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC, (2012•东城区一模)如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足AE=FC=CP=1.将△AEF沿EF折起到△A1EF的位置,使平面A1EF⊥平面EFB,连接A1B,A1P.(如图2)
(2012•东城区一模)如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足AE=FC=CP=1.将△AEF沿EF折起到△A1EF的位置,使平面A1EF⊥平面EFB,连接A1B,A1P.(如图2)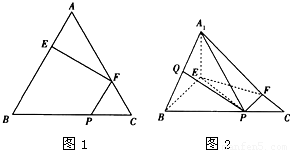 如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足AE=FC=CP=1.将△AEF沿EF折起到△A1EF的位置,使平面A1EF⊥平面EFB,连接A1B,A1P.(如图2)
如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足AE=FC=CP=1.将△AEF沿EF折起到△A1EF的位置,使平面A1EF⊥平面EFB,连接A1B,A1P.(如图2)