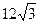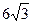题目内容
已知△ABC内接于单位圆,且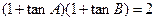 ,
,
(1)求证内角C为定值;(2)求△ABC面积的最大值.
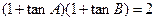 ,
,(1)求证内角C为定值;(2)求△ABC面积的最大值.
(1)∠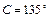 ;(2)
;(2) 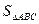 最大值=
最大值=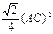 =
= 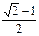
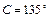 ;(2)
;(2) 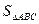 最大值=
最大值=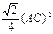 =
= 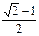
(1)由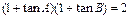
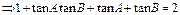
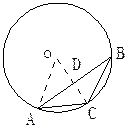
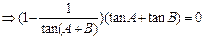
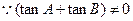
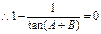
即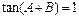 ,所以∠
,所以∠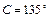
(2)[解析]:由题意可得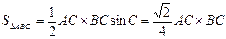
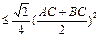
当AC=BC时,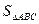 有最大值,最大值为
有最大值,最大值为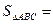
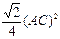
再作辅助线如图,连结OD,OA,得AB⊥OC,
所以AD="BD="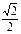 ,CD=1-
,CD=1-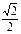 ,
,
AC2=AD2+CD2=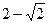 所以
所以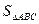 最大值=
最大值=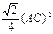 =
= 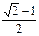
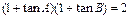
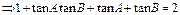
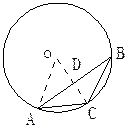
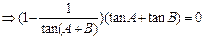
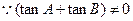
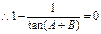
即
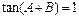 ,所以∠
,所以∠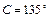
(2)[解析]:由题意可得
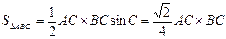
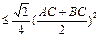
当AC=BC时,
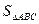 有最大值,最大值为
有最大值,最大值为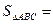
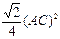
再作辅助线如图,连结OD,OA,得AB⊥OC,
所以AD="BD="
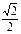 ,CD=1-
,CD=1-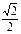 ,
,AC2=AD2+CD2=
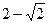 所以
所以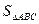 最大值=
最大值=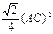 =
= 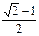

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
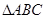 中,若
中,若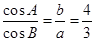 ,则
,则 ,则
,则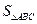 的最大值 。
的最大值 。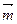 =(cos
=(cos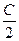 ,sin
,sin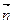 =(cos
=(cos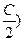 且
且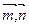 的夹角为
的夹角为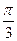
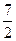 ,三角形的面积S=
,三角形的面积S= ,求a+b(a、b、c分别∠A、∠B、∠C所对的边)
,求a+b(a、b、c分别∠A、∠B、∠C所对的边) ,
,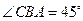 ,且
,且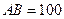 米。
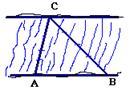
米。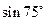 ;
;
 中,
中,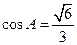 ,
,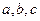 分别是角
分别是角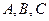 所对的边.
所对的边.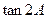 ; (Ⅱ)若
; (Ⅱ)若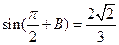 ,
,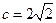 ,求
,求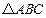 中,
中,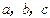 分别是三个内角
分别是三个内角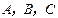 的对边.若
的对边.若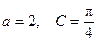 ,
,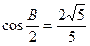 ,
,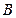 的余弦值;
的余弦值;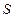 .
.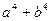
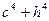 的大小关系是 ( )
的大小关系是 ( )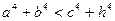 B.
B.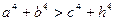
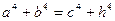 D.不能确定
D.不能确定