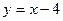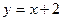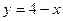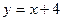题目内容

函数f（x）=ax3+bx2+cx+d的图象如图所示，那么（　　）
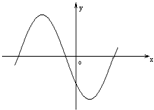
A．a＜0，b＞0，c＞0B．a＞0，b＞0，c＜0
C．a＜0，b＞0，c＜0D．a＞0，b＜0，c＞0

由函数f（x）的图象知f（x）先递增，再递减，再递增
∴f′（x）先为正，再变为负，再变为正
∵f′（x）=3ax2+2bx+c
∴a＞0
∵在递减区间内
∴f′（0）＜0，即c＜0
故选B．
练习册系列答案
相关题目
现有四个函数：①y=x•sinx②y=x•cosx③y=x•|cosx|④y=x•2x的图象（部分）如下，则按照从左到右图象对应的函数序号安排正确的一组是（　　）
A．①④③②B．④①②③C．①④②③D．③④②①





A．B．
C．D．
将直线l沿x轴正方向平移2个单位，再沿y轴负方向平移3个单位，又回到了原来的位置，则l的斜率是（　　）
A．
3
2
B．-
3
2
C．
2
3
D．-
2
3
设函数f（x）=|x2-2x|．
（1）画出f（x）=|x2-2x|在区间[-1，4]上函数f（x）的图象；并根据图象写出该函数在[-1，4]上的单调区间；
（2）试讨论方程f（x）=a在区间[-1，4]上实数根的情况，并加以简要说明．
设函数f（x）的图象与函数y=2x的图象关于直线y=x对称，则只需将函数y=log2（x+1）的图象作如下变换就能得到函数f（x）的图象（　　）
A．向左平行移动1个单位B．向右平行移动1个单位
C．向上平行移动1个单位D．向下平行移动1个单位
若函数y=f（x）是函数y=ax（a＞0，且a≠1）的反函数，其图象经过点（，a），则f（x）=（　　）
A．log2xB．C．D．x2
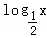
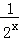
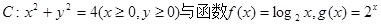已知圆的图象分别交于的值为 （   ）
                                        
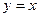把函数的图象F按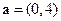，平移到F/，则F/的函数式为（    ）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网