题目内容
抛物线y=x2+bx+c在点（1，2）处的切线与其平行直线bx+y+c=0间的距离是（ ）A．
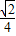
B．
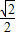
C．
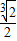
D．
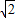
【答案】分析：求出函数f（x）=x2+bx+c在点x=1处的导数值，这个导数值即函数图象在该点处的切线的斜率，然后根据两直线平行的条件列方程求解b，a，最后利用平行直线间的距离求解即可．
解答：解：由题意得：f'（x）=2x+b，
∴f′（1）=2+b，
即函数在点x=1处的切线的斜率是2+b，
∵直线bx+y+c=0的斜率是-b，
所以2+b=-b，解得b=-1．
∵抛物线y=x2+bx+c过点（1，2），∴2=1-1+c，⇒c=2，
故切线x-y-3=0与其平行直线x-y-2=0间的距离是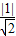
=
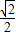
故选B．
点评：本题考查导数的几何意义、两直线平行的条件，把握好这两个知识，列式易求解问题．
解答：解：由题意得：f'（x）=2x+b，
∴f′（1）=2+b，
即函数在点x=1处的切线的斜率是2+b，
∵直线bx+y+c=0的斜率是-b，
所以2+b=-b，解得b=-1．
∵抛物线y=x2+bx+c过点（1，2），∴2=1-1+c，⇒c=2，
故切线x-y-3=0与其平行直线x-y-2=0间的距离是
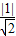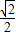
=故选B．
点评：本题考查导数的几何意义、两直线平行的条件，把握好这两个知识，列式易求解问题．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
（2012•大丰市一模）如图所示，已知平面直角坐标系xOy，抛物线y=-x2+bx+c过点A（4，0）、B（1，3）．