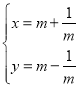题目内容
【题目】已知数列![]() 满足:
满足:![]() (常数
(常数![]() ),
),![]()
![]() .数列
.数列![]() 满足:
满足:![]()
![]() .
.
(1)求![]()
![]()
![]()
![]() 的值;
的值;
(2)求出数列![]() 的通项公式;
的通项公式;
(3)问:数列![]() 的每一项能否均为整数?若能,求出k的所有可能值;若不能,请说明理由.
的每一项能否均为整数?若能,求出k的所有可能值;若不能,请说明理由.
【答案】(1) ![]()
![]() ;(2)
;(2) ![]() ; (3) k为1,2时数列
; (3) k为1,2时数列![]() 是整数列.
是整数列.
【解析】
(1)经过计算可知:![]() ,由数列
,由数列![]() 满足:
满足:![]() (n=1,2,3,4…),从而可求
(n=1,2,3,4…),从而可求![]()
![]()
![]()
![]() ;
;
(2)由条件可知![]() .得
.得![]() ,两式相减整理得
,两式相减整理得![]() ,从而可求数列
,从而可求数列![]() 的通项公式;
的通项公式;
(3)假设存在正数k,使得数列![]() 的每一项均为整数,则由(2)可知:
的每一项均为整数,则由(2)可知: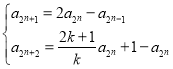 ,由
,由![]() ,
,![]() ,可求得
,可求得![]() .证明
.证明![]() 时,满足题意,说明
时,满足题意,说明![]() 时,数列
时,数列![]() 是整数列.
是整数列.
(1)由已知可知:![]() ,
,
把数列![]() 的项代入
的项代入![]()
求得![]()
![]() ;
;
(2)由![]()
![]()
可知:![]() ①
①
则:![]() ②
②
①②有:![]() ,
,
即:![]()
![]() …
…![]() ,
,![]() …
…![]() ,
,
![]() ;
;
(3)假设存在正数k使得数列![]() 的每一项均为整数,
的每一项均为整数,
则由(2)可知: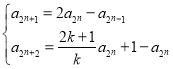 ③,
③,
由![]() ,
,![]() ,可知
,可知![]() ,2.
,2.
当![]() 时,
时,![]() 为整数,利用
为整数,利用![]() 结合③式可知
结合③式可知![]() 的每一项均为整数;
的每一项均为整数;
当![]() 时,③变为
时,③变为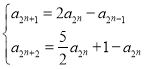 ④
④
用数学归纳法证明![]() 为偶数,
为偶数,![]() 为整数.
为整数.
![]() 时结论显然成立,假设
时结论显然成立,假设![]() 时结论成立,
时结论成立,
这时![]() 为偶数,
为偶数,![]() 为整数,
为整数,
故![]() 为偶数,
为偶数,![]() 为整数,
为整数,
![]() 时,命题成立.
时,命题成立.
故数列![]() 是整数列.
是整数列.
综上所述k为1,2时数列![]() 是整数列.
是整数列.

【题目】微信红包是一款可以实现收发红包、查收记录和提现的手机应用.某网络运营商对甲、乙两个品牌各5种型号的手机在相同环境下抢到的红包个数进行统计,得到如表数据:
手机品牌 |
|
|
|
|
|
甲品牌(个 | 4 | 3 | 8 | 6 | 12 |
乙品牌(个 | 5 | 7 | 9 | 4 | 3 |
手机品牌 | 优 | 非优 | 合计 |
| |||
乙品牌(个 | |||
合计 |
(1)如果抢到红包个数超过5个的手机型号为“优”,否则“非优”,请完成上述![]() 列联表,据此判断是否有
列联表,据此判断是否有![]() 的把握认为抢到的红包个数与手机品牌有关?
的把握认为抢到的红包个数与手机品牌有关?
(2)如果不考虑其它因素,要从甲品牌的5种型号中选出3种型号的手机进行大规模宣传销售.以![]() 表示选中的手机型号中抢到的红包超过5个的型号种数,求随机变量
表示选中的手机型号中抢到的红包超过5个的型号种数,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
下面临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | <>2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]()
![]() ,其中
,其中![]() .
.
【题目】中国北京世界园艺博览会于2019年4月29日至10月7日在北京市延庆区举行.组委会为方便游客游园,特推出“导引员”服务.“导引员”的日工资方案如下:
![]() 方案:由三部分组成
方案:由三部分组成
(表一)
底薪 | 150元 |
工作时间 | 6元/小时 |
行走路程 | 11元/公里 |
![]() 方案:由两部分组成:(1)根据工作时间20元/小时计费;(2)行走路程不超过4公里时,按10元/公里计费;超过4公里时,超出部分按15元/公里计费.已知“导引员”每天上班8小时,由于各种因素,“导引员”每天行走的路程是一个随机变量.试运行期间,组委会对某天100名“导引员”的行走路程述行了统计,为了计算方便对日行走路程进行取整处理.例如行走1.8公里按1公里计算,行走5.7公里按5公里计算.如表所示:
方案:由两部分组成:(1)根据工作时间20元/小时计费;(2)行走路程不超过4公里时,按10元/公里计费;超过4公里时,超出部分按15元/公里计费.已知“导引员”每天上班8小时,由于各种因素,“导引员”每天行走的路程是一个随机变量.试运行期间,组委会对某天100名“导引员”的行走路程述行了统计,为了计算方便对日行走路程进行取整处理.例如行走1.8公里按1公里计算,行走5.7公里按5公里计算.如表所示:
(表二)
行走路程 (公里) |
|
|
|
|
|
人数 | 5 | 10 | 15 | 45 | 25 |
(Ⅰ)分别写出两种方案的日工资![]() (单位:元)与日行走路程
(单位:元)与日行走路程![]() (单位:公里)
(单位:公里)![]() 的函数关系
的函数关系
(Ⅱ)①现按照分层抽样的方工式从![]() ,
,![]() 共抽取5人组成爱心服务队,再从这5人中抽取3人当小红帽,求小红帽中恰有1人来自
共抽取5人组成爱心服务队,再从这5人中抽取3人当小红帽,求小红帽中恰有1人来自![]() 的概率;
的概率;
②“导引员”小张因为身体原因每天只能行走12公里,如果仅从日工资的角度考虑,请你帮小张选择使用哪种方案会使他的日工资更高?