题目内容
(本小题满分14分)
已知函数 .
.
(Ⅰ)函数 在区间
在区间 上是增函数还是减函数?证明你的结论;
上是增函数还是减函数?证明你的结论;
(Ⅱ)当 时,
时, 恒成立,求整数
恒成立,求整数 的最大值;
的最大值;
(Ⅲ)试证明: (
( )。
)。
(Ⅰ) 在区间
在区间 上是减函数;(Ⅱ)
上是减函数;(Ⅱ)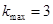 ;
;
(Ⅲ)由(Ⅱ)知:
令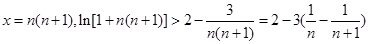 ,
,
由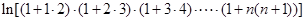
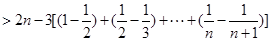
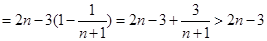
解析试题分析:(Ⅰ)由题 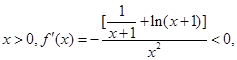 …………(3分)
…………(3分)
故 在区间
在区间 上是减函数 …………………(4分)
上是减函数 …………………(4分)
(Ⅱ)当 时,
时,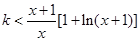 在
在 上恒成立,取
上恒成立,取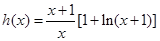 ,则
,则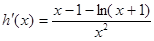 , ……………………(6分)
, ……………………(6分)
再取 则
则 …………(7分)
…………(7分)
故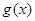 在
在 上单调递增,
上单调递增,
而 ,……………(8分)
,……………(8分)
故 在
在 上存在唯一实数根
上存在唯一实数根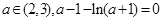 ,
,
故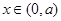 时,
时,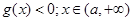 时,
时,
故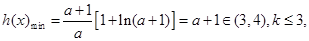 故
故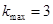 ……………(9分)
……………(9分)
(Ⅲ)由(Ⅱ)知: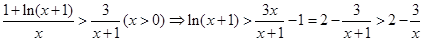
令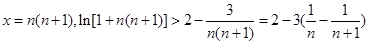 ,
,
又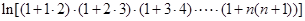
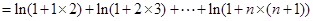
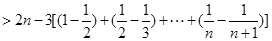
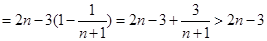
即: ………………(14分)
………………(14分)
考点:本题主要考查应用导数研究函数的单调性及极值,证明不等式。
点评:典型题,本题属于导数应用中的基本问题,(III)通过构造函数,运用“放缩法”转化成数列“裂项相消法”求和,达到证明不等式的目的。本题涉及对数函数,要特别注意函数的定义域。

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 的值域。
的值域。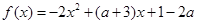 ,
,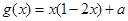 ,其中
,其中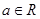 .
. 是偶函数,求函数
是偶函数,求函数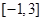 上的最小值;
上的最小值; 时,
时, 上为减函数;
上为减函数;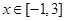 ,函数
,函数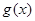 图象上方,求实数
图象上方,求实数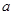 的取值范围.
的取值范围.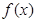 是定义在
是定义在 上的偶函数,已知当
上的偶函数,已知当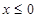 时,
时,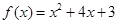 .
.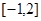 上的值域。
上的值域。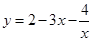 的值域.
的值域. 是定义在
是定义在 上的偶函数,当
上的偶函数,当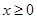 时,
时,
 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 .
. 的解析式;
的解析式; 能作几条直线与曲线
能作几条直线与曲线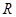 上的函数
上的函数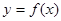 ,
,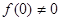 ,当
,当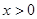 时,
时,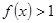 .且对任意的
.且对任意的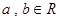 有
有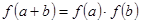 。
。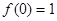 ;
;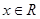 ,恒有
,恒有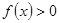 ;
;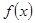 是
是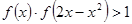 ,求
,求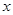 的取值范围。
的取值范围。 ,
, 。
。 的最小正周期和单调递减区间;
的最小正周期和单调递减区间; 上的最小值和最大值,并求出取得最值时
上的最小值和最大值,并求出取得最值时 的值。
的值。