题目内容
若函数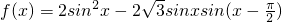 能使得不等式|f(x)-m|<2在区间
能使得不等式|f(x)-m|<2在区间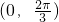 上恒成立,则实数m的取值范围是________.
上恒成立,则实数m的取值范围是________.
(1,2]
分析::利用诱导公式及二倍角、辅助角公式对函数化简可得f(x)=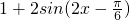 ,由
,由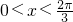 可求sin(2x-
可求sin(2x- )的范围,进而可求f(x)得范围,而|f(x)-m|<2 即m-2<f(x)<2+m在区间
)的范围,进而可求f(x)得范围,而|f(x)-m|<2 即m-2<f(x)<2+m在区间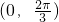 上恒成立可得
上恒成立可得 ,可求
,可求
解答:∵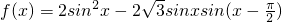
=
=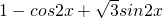 =
=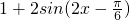
∵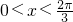 ∴
∴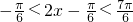
∴ 即0<f(x)≤3
即0<f(x)≤3
∵|f(x)-m|<2 即m-2<f(x)<2+m在区间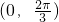 上恒成立
上恒成立
∴ 解可得,1<m≤2
解可得,1<m≤2
故答案为:(1,2]
点评:本题主要考查了函数的恒成立问题的求解,解题的关键是灵活利用三角函数的诱导公式、二倍角公式及辅助角公式对已知函数进行化简,然后结合正弦函数的性质求解.
分析::利用诱导公式及二倍角、辅助角公式对函数化简可得f(x)=
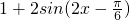 ,由
,由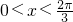 可求sin(2x-
可求sin(2x- )的范围,进而可求f(x)得范围,而|f(x)-m|<2 即m-2<f(x)<2+m在区间
)的范围,进而可求f(x)得范围,而|f(x)-m|<2 即m-2<f(x)<2+m在区间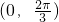 上恒成立可得
上恒成立可得 ,可求
,可求解答:∵
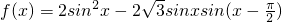
=

=
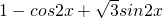 =
=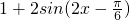
∵
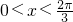 ∴
∴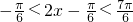
∴
 即0<f(x)≤3
即0<f(x)≤3∵|f(x)-m|<2 即m-2<f(x)<2+m在区间
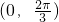 上恒成立
上恒成立∴
 解可得,1<m≤2
解可得,1<m≤2故答案为:(1,2]
点评:本题主要考查了函数的恒成立问题的求解,解题的关键是灵活利用三角函数的诱导公式、二倍角公式及辅助角公式对已知函数进行化简,然后结合正弦函数的性质求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
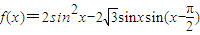 能使得不等式|f(x)-m|<2在区间
能使得不等式|f(x)-m|<2在区间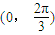 上恒成立,则实数m的取值范围是 .
上恒成立,则实数m的取值范围是 .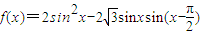 能使得不等式|f(x)-m|<2在区间
能使得不等式|f(x)-m|<2在区间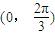 上恒成立,则实数m的取值范围是 .
上恒成立,则实数m的取值范围是 .