题目内容
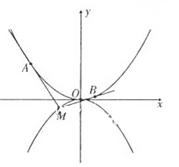
如图,抛物线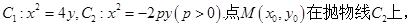
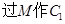
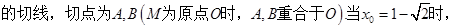


(I)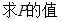 ;
;
(II)
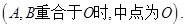
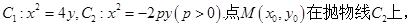
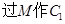
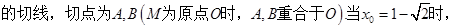


(I)
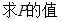 ;
;(II)
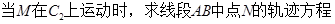
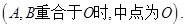
(I)p=2(II)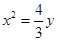
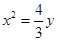
(I)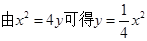 ,该抛物线上任意一点的切线斜率为
,该抛物线上任意一点的切线斜率为
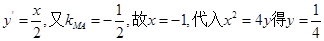 ,即
,即
故,切线MA的方程为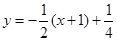 ,又因为点
,又因为点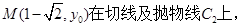
 ,代入抛物线得
,代入抛物线得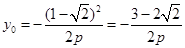
联立解得p=2
(II)设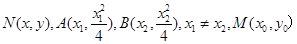 ,由N为线段AB的中点可得
,由N为线段AB的中点可得
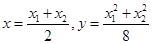 ,切线MA,MB的方程为
,切线MA,MB的方程为
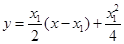 ,
, ,两式联立求得交点M的坐标
,两式联立求得交点M的坐标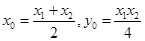
由 ,再由
,再由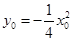
可得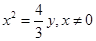 ,经检验当A,B重合于坐标原点是方程也满足,因此AB中点N的轨迹方程为
,经检验当A,B重合于坐标原点是方程也满足,因此AB中点N的轨迹方程为
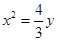
第一小题主要是要求学生把题目所给的抛物线方程转化成二次函数,从而想到切线的斜率即为该点的导数值,求得切点坐标,写出切线方程,进而求得p的值。
第二小题主要是寻找点M与点N的关系,通过设出各点的坐标,充分利用点在曲线上及他们之间的关系,代入建立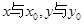 间的关系,最后运用点M在已知曲线上求得x与y的关系。本题在求解过程中注意整体消参的方法。最后不要漏掉对特殊点即原点的考虑。
间的关系,最后运用点M在已知曲线上求得x与y的关系。本题在求解过程中注意整体消参的方法。最后不要漏掉对特殊点即原点的考虑。
【考点定位】本题考查抛物线的性质,导数的意义,曲线的方程,整体代入消参求动点的轨迹。
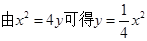 ,该抛物线上任意一点的切线斜率为
,该抛物线上任意一点的切线斜率为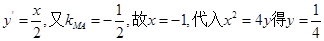 ,即
,即
故,切线MA的方程为
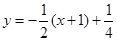 ,又因为点
,又因为点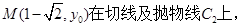
 ,代入抛物线得
,代入抛物线得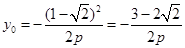
联立解得p=2
(II)设
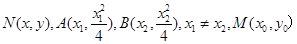 ,由N为线段AB的中点可得
,由N为线段AB的中点可得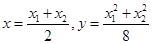 ,切线MA,MB的方程为
,切线MA,MB的方程为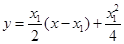 ,
, ,两式联立求得交点M的坐标
,两式联立求得交点M的坐标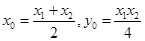
由
 ,再由
,再由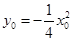
可得
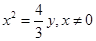 ,经检验当A,B重合于坐标原点是方程也满足,因此AB中点N的轨迹方程为
,经检验当A,B重合于坐标原点是方程也满足,因此AB中点N的轨迹方程为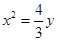
第一小题主要是要求学生把题目所给的抛物线方程转化成二次函数,从而想到切线的斜率即为该点的导数值,求得切点坐标,写出切线方程,进而求得p的值。
第二小题主要是寻找点M与点N的关系,通过设出各点的坐标,充分利用点在曲线上及他们之间的关系,代入建立
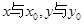 间的关系,最后运用点M在已知曲线上求得x与y的关系。本题在求解过程中注意整体消参的方法。最后不要漏掉对特殊点即原点的考虑。
间的关系,最后运用点M在已知曲线上求得x与y的关系。本题在求解过程中注意整体消参的方法。最后不要漏掉对特殊点即原点的考虑。【考点定位】本题考查抛物线的性质,导数的意义,曲线的方程,整体代入消参求动点的轨迹。

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
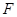 为抛物线
为抛物线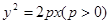 的焦点,抛物线上点
的焦点,抛物线上点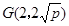 满足
满足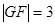

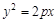 的方程;
的方程;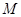 点的坐标为(
点的坐标为(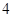 ,
, ),过点F作斜率为
),过点F作斜率为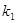 的直线与抛物线交于
的直线与抛物线交于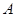 、
、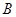 两点,
两点,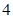 ,连结
,连结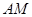 、
、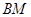 并延长交抛物线于
并延长交抛物线于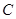 、
、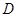 两点,设直线
两点,设直线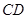 的斜率为
的斜率为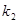 ,问
,问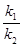 是否为定值,若是求出该定值,若不是说明理由.
是否为定值,若是求出该定值,若不是说明理由.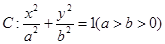 的离心率为
的离心率为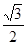 ,双曲线
,双曲线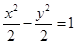 的渐近线与椭圆有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆的方程为( )
的渐近线与椭圆有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆的方程为( )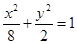
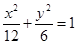
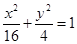
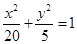
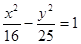 的左焦点为
的左焦点为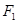 ,点
,点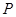 为双曲线右支上一点,且
为双曲线右支上一点,且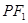 与圆
与圆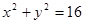 相切于点
相切于点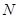 ,
,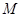 为线段
为线段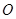 为坐标原点, 则
为坐标原点, 则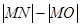 =
= 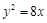 的准线过双曲线
的准线过双曲线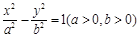 的一个焦点, 且双曲线的离心率为2, 则该双曲线的方程为 .
的一个焦点, 且双曲线的离心率为2, 则该双曲线的方程为 .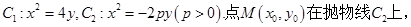

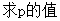 ;
;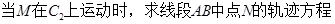

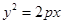 的焦点坐标为
的焦点坐标为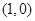 ,则
,则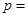 ____;准线方程为_____.
____;准线方程为_____.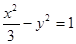 与抛物线
与抛物线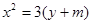 相交于
相交于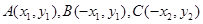
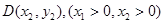 ,直线AC、BD的交点为P(0,p)。
,直线AC、BD的交点为P(0,p)。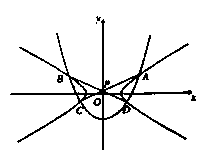
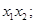
 和双曲线
和双曲线 有相同的焦点F1、F2,以线段F1F2为边作正△F1F2M,若椭圆与双曲线的一个交点P恰好是MF1的中点,设椭圆和双曲线的离心率分别为
有相同的焦点F1、F2,以线段F1F2为边作正△F1F2M,若椭圆与双曲线的一个交点P恰好是MF1的中点,设椭圆和双曲线的离心率分别为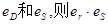 等于
等于