题目内容
事件A发生的概率记为P(A),事件A的对立事件记为 ,那么,下列命题中正确命题的个数是
,那么,下列命题中正确命题的个数是
①P(A+B)=P(A)+P(B);
②P(A+ )=P(A)+P(
)=P(A)+P( );
);
③P(A∪ )=1;
)=1;
④若P(A)=1,则事件A一定是必然事件.
- A.1
- B.2
- C.3
- D.4
B
分析:①若事件A、B不互斥,则不成立;
②由事件A与 互斥即可判断出;
互斥即可判断出;
③由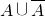 =Ω及P(Ω)=1即可判断出;
=Ω及P(Ω)=1即可判断出;
④举反例:几何概型或连续型随机变量的概率即可判断出.
解答:①只有当事件A、B互斥时,式子P(A+B)=P(A)+P(B)才成立,因此①不正确;
②∵事件A与 互斥,故P(A+
互斥,故P(A+ )=P(A)+P(
)=P(A)+P( )成立;
)成立;
③∵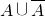 =Ω,∴
=Ω,∴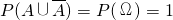 成立;
成立;
④若P(A)=1,则事件A不一定是必然事件,例如几何概型和连续型随机事件的概率在某一个点的概率皆为0,若事件A表示是去掉某一个点的事件,显然事件A≠Ω,因此④不正确.
综上可知:只有②③正确.
因此正确命题的个数是2.
故选B.
点评:正确理解互斥事件、对立事件及连续型事件的概率的意义与概率的性质是解题的关键.
分析:①若事件A、B不互斥,则不成立;
②由事件A与
 互斥即可判断出;
互斥即可判断出;③由
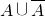 =Ω及P(Ω)=1即可判断出;
=Ω及P(Ω)=1即可判断出;④举反例:几何概型或连续型随机变量的概率即可判断出.
解答:①只有当事件A、B互斥时,式子P(A+B)=P(A)+P(B)才成立,因此①不正确;
②∵事件A与
 互斥,故P(A+
互斥,故P(A+ )=P(A)+P(
)=P(A)+P( )成立;
)成立;③∵
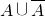 =Ω,∴
=Ω,∴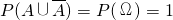 成立;
成立;④若P(A)=1,则事件A不一定是必然事件,例如几何概型和连续型随机事件的概率在某一个点的概率皆为0,若事件A表示是去掉某一个点的事件,显然事件A≠Ω,因此④不正确.
综上可知:只有②③正确.
因此正确命题的个数是2.
故选B.
点评:正确理解互斥事件、对立事件及连续型事件的概率的意义与概率的性质是解题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 ,那么,下列命题中正确命题的个数是( )
,那么,下列命题中正确命题的个数是( ) )=P(A)+P(
)=P(A)+P( );
); )=1;
)=1; ,那么,下列命题中正确命题的个数是( )
,那么,下列命题中正确命题的个数是( ) )=P(A)+P(
)=P(A)+P( );
); )=1;
)=1;