题目内容
记事件A=“直线ax-by=0与圆(x-2)2+y2=1相交”.
(Ⅰ)若将一颗骰子投掷两次得到的点数分别为a、b,求事件A发生的概率;
(Ⅱ)若实数a、b满足(a-2)2+(b-
)2<1,求事件A发生的概率.
(Ⅰ)若将一颗骰子投掷两次得到的点数分别为a、b,求事件A发生的概率;
(Ⅱ)若实数a、b满足(a-2)2+(b-
| 3 |
分析:(Ⅰ)由题意可得:故b>
a,可列举得到方法种数,进而可得所要求的概率;
(Ⅱ)首先确定为几何概型,然后分别求两个面积可得答案.
| 3 |
(Ⅱ)首先确定为几何概型,然后分别求两个面积可得答案.
解答:解:(Ⅰ)由题意可得:直线ax-by=0与圆(x-2)2+y2=1相交,
所以圆心(2,0)到直线的距离d=
<1,即3a2<b2,
又a、b均大于0,故b>
a,
当a=1时,b=2,3,4,5,6;当a=2时,b=4,5,6;当a=3时,b=6,
故事件A发生的方法种数为9,而总的方法种数为6×6=36
故事件A发生的概率为P=
=
(Ⅱ)依题意为几何概型,b>
a与(a-2)2+(b-
)2<1的公共面积为
直线b=
a与圆(a-2)2+(b-
)2=1相交的弓形的面积,由点到直线的距离公式可得:
圆心到直线的距离d′=
=
,故扇形的中心角为
,
则弓形的面积S=
π12-
12=
,
故所求的概率为:
=
所以圆心(2,0)到直线的距离d=
| |2a| | ||
|
又a、b均大于0,故b>
| 3 |
当a=1时,b=2,3,4,5,6;当a=2时,b=4,5,6;当a=3时,b=6,
故事件A发生的方法种数为9,而总的方法种数为6×6=36
故事件A发生的概率为P=
| 9 |
| 36 |
| 1 |
| 4 |
(Ⅱ)依题意为几何概型,b>
| 3 |
| 3 |
直线b=
| 3 |
| 3 |
圆心到直线的距离d′=
|2
| ||||
| 2 |
| ||
| 2 |
| π |
| 3 |
则弓形的面积S=
| 1 |
| 6 |
| ||
| 4 |
2π-3
| ||
| 12 |
故所求的概率为:
| ||||
| π |
2π-3
| ||
| 12π |
点评:本题考查古典型和几何概型,分清两种概型是解决问题的关键,属基础题.

练习册系列答案
相关题目
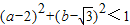 ,求事件A发生的概率.
,求事件A发生的概率.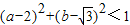 ,求事件A发生的概率.
,求事件A发生的概率.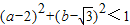 ,求事件A发生的概率.
,求事件A发生的概率.