题目内容
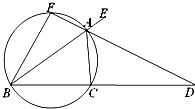（2013•怀化三模）如图，已知AD是△ABC的外角∠EAC的平分线，交BC的延长线于点D，延长DA交△ABC的外接圆于点F，∠BFA=90°，∠EAC=120°，BC=6cm，则AD的长=4
| 3 |
4
．| 3 |
分析：AD是△ABC的外角∠EAC的平分线，∠EAC=120°，可得∠CAD=∠EAD=∠EAB=60°，∠BAC=60°．
由∠BFA=90°，可得AB是此圆的直径，因此∠ACB=90°．即可得到AB=
，可得∠D=∠FAB-∠ABC=30°．进而求得AD．
由∠BFA=90°，可得AB是此圆的直径，因此∠ACB=90°．即可得到AB=
| BC |
| sin60° |
解答：解：∵AD是△ABC的外角∠EAC的平分线，∠EAC=120°，∴∠CAD=∠EAD=∠EAB=60°，
∴∠BAC=60°．
∵∠BFA=90°，∴AB是此圆的直径，
∴∠ACB=90°．
∴AB=
=
=4
．
∵∠D=∠FAB-∠ABC=30°．
∴AD=AB=4
．
故答案为4
．
∴∠BAC=60°．
∵∠BFA=90°，∴AB是此圆的直径，
∴∠ACB=90°．
∴AB=
| BC |
| sin60° |
| 6 | ||||
|
| 3 |
∵∠D=∠FAB-∠ABC=30°．
∴AD=AB=4
| 3 |
故答案为4
| 3 |
点评：熟练角平分线的性质、圆的性质、直角三角形的边角关系、等腰三角形的性质等是解题的关键．
练习册系列答案
发散思维新课堂系列答案
相关题目
（2013•怀化三模）一个空间几何体的正视图、侧视图为两个边长是1的正方形，俯视图是直角边长为1的等腰直角三角形，则这个几何体的表面积等于（ ）