题目内容
甲乙丙三人商量周末去玩,甲提议去市中心逛街,乙提议去城郊觅秋,丙表示随意.最终,商定以抛硬币的方式决定结果.规则是:由丙抛掷硬币若干次,若正面朝上则甲得一分乙得零分,反面朝上则乙得一分甲得零分,先得4分者获胜,三人均执行胜者的提议.记所需抛币次数为ξ.
(1)求ξ=6的概率;
(2)求ξ的分布列和期望.
(1)求ξ=6的概率;
(2)求ξ的分布列和期望.
分析:(1)先确定ξ=6的意义,首先可以分析得到甲赢或乙赢的概率均为
,若第6次甲赢意味着“第6次甲赢,前5次赢3次,但根据规则,前4次中必输1次”.若乙赢同样.故可根据二项分布列出式子求解即可.
(2)确定ξ的所有可能取值,求出相应的概率,即可求随机变量ξ的分布列和数学期望.
| 1 |
| 2 |
(2)确定ξ的所有可能取值,求出相应的概率,即可求随机变量ξ的分布列和数学期望.
解答:解:(1)当ξ=6时,若甲赢意味着“第6次甲赢,前5次赢3次,
但根据规则,前4次中必输1次”,由规则,每次甲赢或乙赢的概率均为
,
因此P(ξ=6)=2
×(
)3×(
)2×
=
…4分
(2)分布列为:
…10分
∴Eξ=4×
+5×
+6×
+7×
=
…12分
但根据规则,前4次中必输1次”,由规则,每次甲赢或乙赢的概率均为
| 1 |
| 2 |
因此P(ξ=6)=2
| C | 3 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 16 |
(2)分布列为:
| ξ | 4 | 5 | 6 | 7 | ||||||||
| P |
|
|
|
|
∴Eξ=4×
| 1 |
| 8 |
| 1 |
| 4 |
| 5 |
| 16 |
| 5 |
| 16 |
| 93 |
| 16 |
点评:本小题主要考查离散型随机变量及其分布列,古典概型,独立重复试验,数学期望等知识,考查随机思想以及数据处理能力、抽象思维能力、运算求解能力和应用意识.

练习册系列答案
相关题目
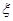 .
.