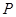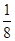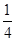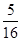题目内容
甲乙丙三人商量周末去玩，甲提议去市中心逛街，乙提议去城郊觅秋，丙表示随意。最终，商定以抛硬币的方式决定结果。规则是：由丙抛掷硬币若干次，若正面朝上则甲得一分乙得零分，反面朝上则乙得一分甲得零分，先得4分者获胜，三人均执行胜者的提议.记所需抛币次数为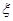
.
⑴求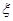=6的概率；
⑵求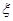的分布列和期望.
【答案】
（1）
；（2）
.
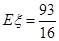【解析】
试题分析：（1）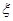
=6说明前5次中恰有3次胜2次负，第6次一定是胜，而且甲乙两人均有可能胜；
（2）将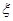的取值分析明白：
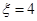说明4次比赛均胜；
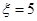说明第5次一定胜，前4次中3胜1负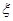；=6说明前5次中恰有3次胜2次负，第6次一定是胜;
说明第7次一定胜，前6次中3胜3负.
试题解析：(1)
4分
(2)分布列为:
|
|
4 |
5 |
6 |
7 |
|
|
|
|
|
|
10分
∴
.
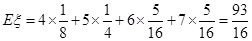12分
考点：1.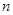 
次独立事件中某事件恰好发生
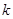次的概率公式；2.互斥事件概率加法；3.离散型随机变量的分布列.
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
.