题目内容
如图所示,过正方形ABCD的顶点A,作PA⊥平面AB-CD,设PA=AB=a.

(1)求二面角B-PC-D的大小;
(2)求平面PAB和平面PCD所成二面角的大小.
答案:
解析:
解析:
|
(1)如图,∵PA⊥平面ABCD,BD⊥AC,∴BD⊥PC,在平面PBC内,作BE⊥PC,E为垂足,连接DE,得PC⊥平面BED,从而DE⊥PC,即∠BED是二面角B-PC-D的平面角,在Rt△PAB中,由PA=PB=a,得PB=
(2)过P作PQ∥AB,则PQ |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .∵PA⊥平面ABCD,BC⊥AB,∴BC⊥PB.∴PC=
.∵PA⊥平面ABCD,BC⊥AB,∴BC⊥PB.∴PC= .在Rt△PBD中,BE=
.在Rt△PBD中,BE= ;同理DE=
;同理DE= a.在△BDE中,根据余弦定理,cos∠BED=
a.在△BDE中,根据余弦定理,cos∠BED= .∴∠BED=
.∴∠BED= ,此即为二面角B-PC-D的大小.
,此即为二面角B-PC-D的大小.
 平面PAB.∵AB∥CD,∴PQ∥CD.PQ
平面PAB.∵AB∥CD,∴PQ∥CD.PQ ,即,平面PAB和PCD所成的二面角是
,即,平面PAB和PCD所成的二面角是 如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.
如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.
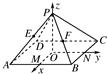 如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.
如图所示,过正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的边长为2,OP=2,连接AP、BP、CP、DP,M、N分别是AB、BC的中点,以O为原点,射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系.若E、F分别为PA、PB的中点,求A、B、C、D、E、F的坐标.