题目内容
锐角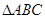 中,角
中,角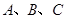 所对的边分别为
所对的边分别为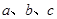 ,
,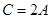 ,
,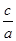 的取值范围是( )
的取值范围是( )
A.(1,2) B.(1,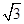 ) c.(
) c.(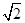 ,2) D.(
,2) D.(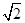 ,
,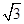 )
)
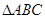 中,角
中,角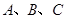 所对的边分别为
所对的边分别为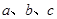 ,
,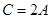 ,
,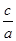 的取值范围是( )
的取值范围是( )A.(1,2) B.(1,
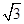 ) c.(
) c.(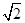 ,2) D.(
,2) D.(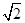 ,
,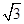 )
)D
分析:由题意可得 0<2A< ,且
,且  <3A<π,解得A的范围,可得cosA的范围,由正弦定理求得
<3A<π,解得A的范围,可得cosA的范围,由正弦定理求得  =2cosA,解得所求.
=2cosA,解得所求.
解答:解:锐角△ABC中,角A、B、C所对的边分别为a、b、c,C=2A,∴0<2A< ,且
,且  <3A<π.
<3A<π.
∴ <A<
<A< ,
,
∴ <cosA<
<cosA< . 由正弦定理可得
. 由正弦定理可得  =
= =2cosA,∴
=2cosA,∴ <2cosA<
<2cosA< ,
,
故选 D.
 ,且
,且  <3A<π,解得A的范围,可得cosA的范围,由正弦定理求得
<3A<π,解得A的范围,可得cosA的范围,由正弦定理求得  =2cosA,解得所求.
=2cosA,解得所求.解答:解:锐角△ABC中,角A、B、C所对的边分别为a、b、c,C=2A,∴0<2A<
 ,且
,且  <3A<π.
<3A<π.∴
 <A<
<A< ,
,∴
 <cosA<
<cosA< . 由正弦定理可得
. 由正弦定理可得  =
= =2cosA,∴
=2cosA,∴ <2cosA<
<2cosA< ,
,故选 D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 方向移动,离台风中心30千米内的地区为危险区,城市B在A的正东30千米处,B城市处于危险区内的时间共有
方向移动,离台风中心30千米内的地区为危险区,城市B在A的正东30千米处,B城市处于危险区内的时间共有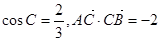 且
且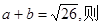 c等于 ( )
c等于 ( )
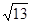
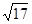
 中,
中, 、
、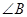 、
、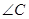 的对边分别为
的对边分别为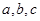 若
若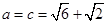 且
且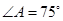 ,则
,则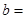 ( )
( )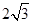
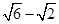
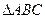 中,角
中,角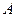 、
、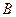 、
、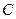 的对边分别为
的对边分别为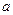 、
、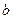 、
、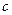 ,且
,且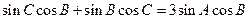 。
。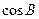 的值;
的值;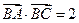 ,且
,且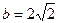 ,求
,求 B,C为锐角
B,C为锐角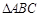 的三个内角,向量
的三个内角,向量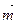
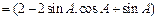 ,
,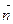
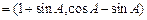 ,且
,且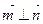 .
.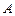 的大小;
的大小;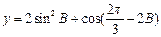 取最大值时角
取最大值时角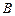 的大小.
的大小.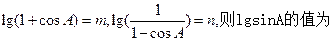 ( )
( )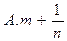
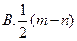
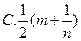
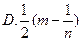
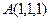 ,
, ,
,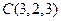 ,则△ABC的面积是 .
,则△ABC的面积是 .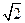 ,b=2,sinB+cosB=
,b=2,sinB+cosB=