题目内容
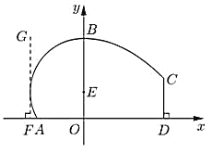
【题目】函数 y f(x) 的定义域为[2.1,2],其图像如下图所示,且 f(2.1) 0.96
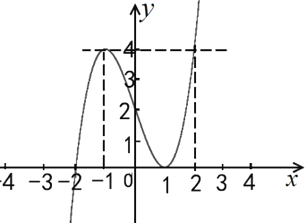
(1)若函数 yf(x) k恰有两个不同的零点,则 k_____
(2)已知函数 g ( x) ![]() , yg[f(x)] 有_____个不同的零点
, yg[f(x)] 有_____个不同的零点
【答案】4或0 4
【解析】
(1)函数 yf(x) k恰有两个不同的零点等价于y=f(x)和y=k的图象有两个不同的交点,再结合图像即可得解;
(2)先由函数g(x)![]() ,求得函数g(x)的零点
,求得函数g(x)的零点![]() ,再求解
,再求解![]() 的解的个数即可.
的解的个数即可.
解:(1)∵y=f(x)﹣k恰有两个不同的零点,
∴y=f(x)和y=k图象有两个不同的交点.
又y=f(x)的图象如图:由图可得:当y=f(x)和y=k图象有两个不同的交点时,
k=4或k=0.
(2)∵g(x)![]() ,
,
当x≤0时,2x+1=0,得x![]() ;
;
此时f(x)![]() ,由图可知有一个解;
,由图可知有一个解;
当x>0时,g(x)=x3+2x﹣16单调递增,
∵g(2)=﹣4,g(3)=17,
∴g(x)在(2,3)有一个零点x0,即f(x)=x0∈(2,3)
由图可知有三个解,
∴共有四个解.
故答案为(1). 4或0 (2). 4

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目