题目内容
如图,已知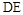
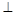 平面
平面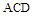 ,
,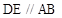 ,
,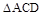 是正三角形,AD=DE
是正三角形,AD=DE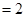 AB,且F是CD的中点.
AB,且F是CD的中点.
⑴求证:AF//平面BCE;
⑵求证:平面BCE⊥平面CDE.
(1)详见解析;⑵详见解析.
解析试题分析:(1)要证AF//平面BCE就需要在平面BCE内找一条直线与AF平行.
取CE中点P,易证ABPF为平行四边形,从而问题得证.
⑵证面面垂直,首先考虑评点哪条线垂直哪个面.
很容易得,AF⊥CD,故考虑证明AF⊥平面CDE.那么需要在平面CDE内再找一条直线与AF垂直.找哪一条呢? ∵DE⊥平面ACD, AF 平面ACD,∴DE⊥AF,这样便可使问题得证.
平面ACD,∴DE⊥AF,这样便可使问题得证.
试题解析:(1)取CE中点P,连结FP、BP。
∵F为CD的中点,∴FP//DE,且FP=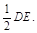 2分
2分
又AB//DE,且AB= ∴AB//FP,且AB=FP,
∴AB//FP,且AB=FP,
∴ABPF为平行四边形,∴AF//BP.
又∵AF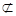 平面BCE,BP
平面BCE,BP 平面BCE,∴AF//平面BCE. 6分
平面BCE,∴AF//平面BCE. 6分
⑵∵△ACD为正三角形,∴AF⊥CD.
∵DE⊥平面ACD, AF 平面ACD,
平面ACD,
∴DE⊥AF
又AF⊥CD,CD∩DE=D,
∴AF⊥平面CDE. 8分
又BP//AF,∴BP⊥平面CDE。 10分
又∵BP 平面BCE,
平面BCE,
∴平面BCE⊥平面CDE. 12分
考点:空间直线与平面的位置关系.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
 中,
中,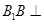 平面
平面 ,
, ,
,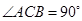 ,
, 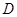 ,
, 分别是
分别是 ,
, 的中点.
的中点.
 ∥平面
∥平面 ;
; 平面
平面 ;
; 与平面
与平面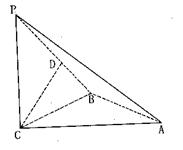
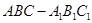 中,
中,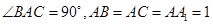 ,
,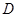 是棱
是棱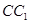 上的一点,
上的一点,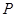 是
是 的延长线与
的延长线与 的延长线的交点,且
的延长线的交点,且 ∥平面
∥平面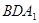 。
。
 ;
; 的平面角的余弦值;
的平面角的余弦值; 到平面
到平面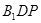 的距离.
的距离. 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD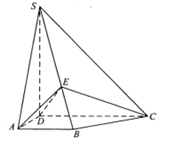
 ;
; ,当平面EDC
,当平面EDC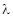 的值;
的值;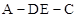 的大小.
的大小.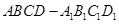 的底面
的底面 是平行四边形,且
是平行四边形,且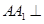 底面
底面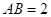 ,
,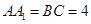 ,
,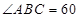 °,点
°,点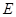 为
为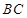 中点,点
中点,点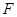 为
为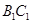 中点.
中点.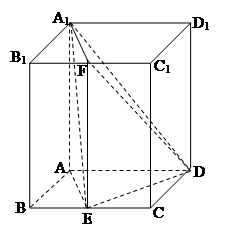
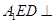 平面
平面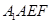 ;
;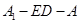 的大小为
的大小为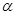 ,直线
,直线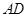 与平面
与平面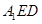 所成的角为
所成的角为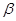 ,求
,求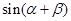 的值.
的值.
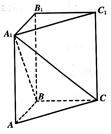
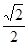 ,求点A到平面A1BC的距离.
,求点A到平面A1BC的距离.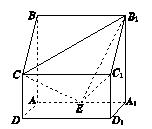
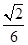 .求线段AM的长.
.求线段AM的长.