题目内容
(本大题满分14分)
已知函数 ,其中
,其中 ,b∈R且b≠0。
,b∈R且b≠0。
(1)求 的单调区间;
的单调区间;
(2)当b=1时,若方程 没有实根,求a的取值范围;
没有实根,求a的取值范围;
(3)证明: ,其中
,其中 .
.
已知函数
 ,其中
,其中 ,b∈R且b≠0。
,b∈R且b≠0。(1)求
 的单调区间;
的单调区间;(2)当b=1时,若方程
 没有实根,求a的取值范围;
没有实根,求a的取值范围;(3)证明:
 ,其中
,其中 .
. 解:(1)由题意可知: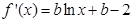 ,b≠0时,
,b≠0时,
令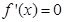 ,得
,得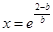 , (1分)
, (1分)
则①b>0,当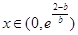 时,
时,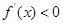 ,
, 单调递减;
单调递减;
当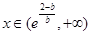 时,
时,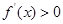 ,
, 单调递增 (3分)②b<0,当
单调递增 (3分)②b<0,当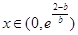 时,
时,
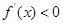 ,
, 单调递增;
单调递增;
当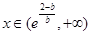 时,
时,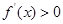 ,
, 单调递减 (5分)
单调递减 (5分)
(2)由(1)可得 在
在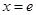 处取得极小值,且
处取得极小值,且 没有实根, (7分)
没有实根, (7分)
则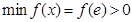 ,即
,即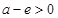 ,解得:
,解得: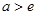 (8分)
(8分)
(3)方法1:由(2)得,令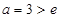 ,
,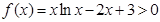 成立,
成立,
则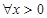 ,
,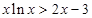 恒成立 (10分)
恒成立 (10分)
故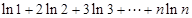
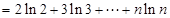
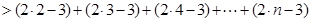
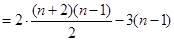
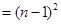 ,即得证。
,即得证。  (14分)
(14分)
方法2:数学归纳法
(1) 当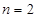 时,
时,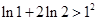 成立;
成立;
(2) 当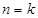 时,
时,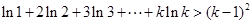 成立,
成立,
当 时,
时,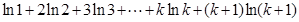
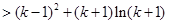
同理令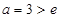 ,
,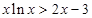 ,即
,即 , (10分)
, (10分)
则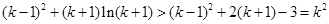 , (12分)
, (12分)
故 ,
,
即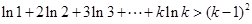 对
对 也成立,
也成立,
综合(1)(2)得: ,
,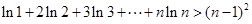 恒成立。 (14分)
恒成立。 (14分)
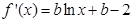 ,b≠0时,
,b≠0时,令
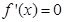 ,得
,得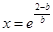 , (1分)
, (1分)则①b>0,当
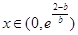 时,
时,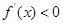 ,
, 单调递减;
单调递减; 当
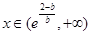 时,
时,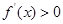 ,
, 单调递增 (3分)②b<0,当
单调递增 (3分)②b<0,当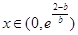 时,
时,
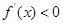 ,
, 单调递增;
单调递增; 当
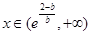 时,
时,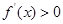 ,
, 单调递减 (5分)
单调递减 (5分)(2)由(1)可得
 在
在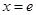 处取得极小值,且
处取得极小值,且 没有实根, (7分)
没有实根, (7分)则
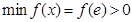 ,即
,即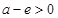 ,解得:
,解得: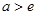 (8分)
(8分)(3)方法1:由(2)得,令
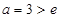 ,
,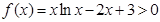 成立,
成立,则
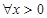 ,
,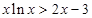 恒成立 (10分)
恒成立 (10分)故
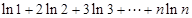
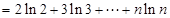
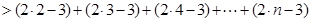
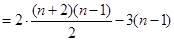
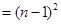 ,即得证。
,即得证。  (14分)
(14分)方法2:数学归纳法
(1) 当
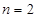 时,
时,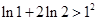 成立;
成立;(2) 当
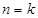 时,
时,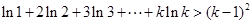 成立,
成立,当
 时,
时,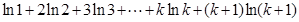
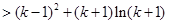
同理令
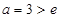 ,
,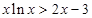 ,即
,即 , (10分)
, (10分)则
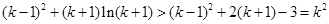 , (12分)
, (12分)故
 ,
,即
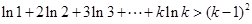 对
对 也成立,
也成立,综合(1)(2)得:
 ,
,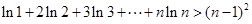 恒成立。 (14分)
恒成立。 (14分)略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的图像(如图所示)过点
的图像(如图所示)过点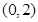 、
、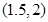 和点
和点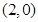 ,且函数图像关于点
,且函数图像关于点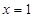 和
和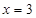 及
及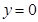 是它的渐近线.现要求根据给出的函数图像研究函数
是它的渐近线.现要求根据给出的函数图像研究函数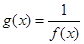 的相关性质与图像,
的相关性质与图像,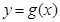 的定义域、值域及单调递增区间;
的定义域、值域及单调递增区间;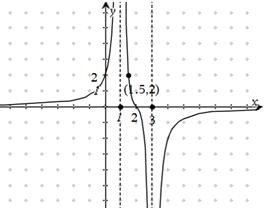
 在
在 处的切线与y轴的交点为 。
处的切线与y轴的交点为 。 ,其中
,其中 .
. 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 时,求
时,求 的单调区间;
的单调区间; 在区间
在区间 内均存在零点.
内均存在零点. 在点(1,1)处的切线与x轴、直线x=2所围成的三角形的面积为_ _。
在点(1,1)处的切线与x轴、直线x=2所围成的三角形的面积为_ _。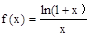
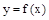 在(0,+
在(0,+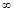 )上的单调性;
)上的单调性;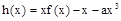 在(0,2)上有极值,求a的取值范围.
在(0,2)上有极值,求a的取值范围. ,则
,则 等于( )
等于( )

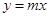 是
是 +1的切线,则
+1的切线,则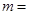 ▲ .
▲ . 在点
在点 处的切线方程为
处的切线方程为 =
=