题目内容
..(本题14分)已知 为常数,且
为常数,且 ,函数
,函数 ,
, (
( ,为自然对数的底数)
,为自然对数的底数)
(Ⅰ)求实数 的值;
的值;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)当 时,是否同时存在实数
时,是否同时存在实数 和
和 (
( <
< ),使得对每一个
),使得对每一个 ,直线
,直线 与曲线
与曲线 (
( )都有公共点?若存在,求出最小的实数
)都有公共点?若存在,求出最小的实数 和最大的实数
和最大的实数 ;若不存在,说明理由.
;若不存在,说明理由.
【答案】
解:(Ⅰ)由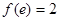 得
得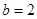 -------------2分
-------------2分
(Ⅱ)由(Ⅰ)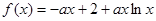 ,∴
,∴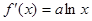 -------------3分
-------------3分
∵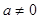 故:
故:
当 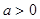 时,由
时,由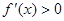 得
得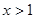 ,由
,由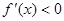 得
得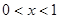 ,
,
当 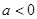 时,由
时,由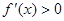 得
得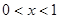 ,由
,由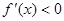 得,
得,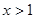 ;
;
综上,当 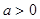 时,
时,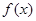 的递增区间为
的递增区间为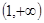 ,递减区间为
,递减区间为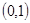 ;----------7分
;----------7分
当 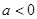 时,
时,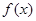 的递增区间为
的递增区间为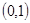 ,递减区间为
,递减区间为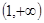 。----------8分
。----------8分
(Ⅲ)当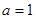 时,
时,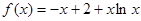 ,
,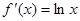
由(Ⅱ)可得,当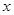 在区间
在区间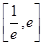 变化时,
变化时,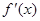 ,
,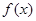 随
随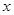 的变化情况如下表:
的变化情况如下表:
|
|
|
|
1 |
|
|
|
|
|
- |
0 |
+ |
|
|
|
|
|
极小值1 |
|
1 |
------------------------------------------11分
又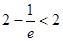 ,所以,函数
,所以,函数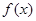 (
(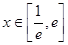 )的值域为
)的值域为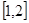 ,--------------12分
,--------------12分
所以,若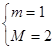 ,则对每一个
,则对每一个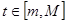 ,直线
,直线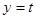 与曲线
与曲线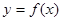 (
(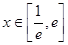 )都有公共点,且对每一个
)都有公共点,且对每一个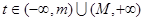 ,直线
,直线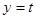 与曲线
与曲线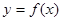 (
(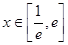 )都没有公共点.
)都没有公共点.
综上,当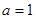 时,存在最小的实数
时,存在最小的实数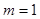 ,最大的实数
,最大的实数 ,使得对每一个
,使得对每一个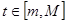 ,直线
,直线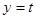 与曲线
与曲线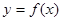 (
(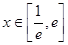 )都有公共点.----------------------14分
)都有公共点.----------------------14分
【解析】略

练习册系列答案
相关题目
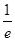
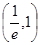
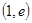
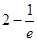
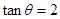
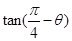 的值;
的值;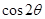 的值.
的值.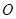 为坐标原点,
为坐标原点,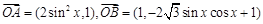 ,
,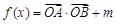 .
.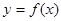 的单调递增区间;
的单调递增区间;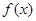 的定义域为
的定义域为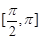 ,值域为
,值域为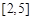 ,求
,求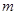 的值.
的值. 是奇函数。(1)求a的值;(2)用定义判断该函数的单调性 (3)若对任意的
是奇函数。(1)求a的值;(2)用定义判断该函数的单调性 (3)若对任意的 ,不等式
,不等式 恒成立,求k的取值范围;
恒成立,求k的取值范围;