题目内容
已知数列{an}是各项均不为0的等差数列,Sn为其前n项和,且满足an2=S2n-1,n∈N+.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)数列{bn}满足bn=
| 1 | anan+1 |
分析:(I)设等差数列{an}的公差为d,首项为a1,然后取n=1,n=2,将等式化成关于a1与d的方程组,解之即可;
(II)将数列的通项进行化简得bn=
=
(
-
),然后进行求和,消项后可求出数列{bn}的前n项和Tn.
(II)将数列的通项进行化简得bn=
| 1 |
| anan+1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
解答:解:(Ⅰ)设等差数列{an}的公差为d,首项为a1,
在an2=S2n-1中,令n=1,n=2,
得
即
(4分)
解得a1=1,d=2,
∴an=2n-1.(6分)
(Ⅱ)∵bn=
=
(
-
),(8分)
∴Tn=
(1-
+
-
+…+
-
)=
. (10分)
在an2=S2n-1中,令n=1,n=2,
得
|
|
解得a1=1,d=2,
∴an=2n-1.(6分)
(Ⅱ)∵bn=
| 1 |
| anan+1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
点评:本题主要考查了数列的通项公式以及利用裂项求和法求数列的和,同时考查了计算能力,属于中档题.

练习册系列答案
相关题目
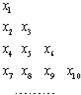 若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足 若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足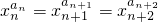 (n∈N*).
(n∈N*).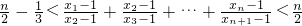 .
. (n∈N*).
(n∈N*). .
.
 (n∈N*).
(n∈N*). .
.