题目内容
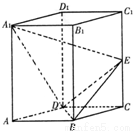
 如图,已知直平行六面体ABCD-A1B1C1D1中,AD⊥BD,AD=BD=a,E是CC1的中点,A1D⊥BE.
如图,已知直平行六面体ABCD-A1B1C1D1中,AD⊥BD,AD=BD=a,E是CC1的中点,A1D⊥BE.(Ⅰ)求证:A1D⊥平面BDE;
(Ⅱ)求二面角B-DE-C的大小;
(Ⅲ)求点B到平面A1DE的距离.
分析:(Ⅰ)由直平行六面体ABCD-A1B1C1D1,可知AA1⊥面ABCD,根据A1D⊥BD,A1D⊥BE,可证A1D⊥平面BDE.
(Ⅱ)过M作MN⊥DE于N,连BN.易证BNM就是二面角B-DE-C的平面角,在Rt△BMN中,可求二面角B-DE-C的大小;
(Ⅲ)易证BN⊥平面A1DE,从而BN的长就是点B到平面A1DE的距离,故可求点B到平面A1DE的距离.
(Ⅱ)过M作MN⊥DE于N,连BN.易证BNM就是二面角B-DE-C的平面角,在Rt△BMN中,可求二面角B-DE-C的大小;
(Ⅲ)易证BN⊥平面A1DE,从而BN的长就是点B到平面A1DE的距离,故可求点B到平面A1DE的距离.
解答:(Ⅰ)证明:∵直平行六面体ABCD-A1B1C1D1中,AA1⊥面ABCD
又∵AD⊥BD,∴A1D⊥BD.…(2分)
又A1D⊥BE,∴A1D⊥平面BDE.…(3分)
(Ⅱ)解:连B1C.∵A1B1∥CD,∴B1C∥A1D.∵A1D⊥BE,∴B1C⊥BE,
∴∠BB1C=∠CBE,∴Rt△BB1C∽Rt△CBE,
∴
=
.∵CE=
BB1,BC=AD=a,∴
B
=BC2=a2,∴BB1=
a.…(5分)
取CD中点M,连BM.∵CD=
a,∴BM=
a.
过M作MN⊥DE于N,连BN.∵平面CD1⊥平面BD,BM⊥CD,∴BM⊥平面CD1,
∴BN⊥DE,∴∠BNM就是二面角B-DE-C的平面角.…(7分)∵sin∠MDN=
=
,DE=
=
=
a,
∴MN=
.在Rt△BMN中,tan∠BNM=
=
,∴∠BNM=arctan
.
即二面角B-DE-C等于arctan
.…(9分)
(Ⅲ)解:∵A1D⊥平面BDE,BN?平面BDE,∴A1D⊥BN.…(10分)
又∵BN⊥DE,∴BN⊥平面A1DE,即BN的长就是点B到平面A1DE的距离.…(11分)
∵BM=
a,MN=
,∴BN=
=
a,
即点B到平面A1DE的距离为
a.…(12分)
又∵AD⊥BD,∴A1D⊥BD.…(2分)
又A1D⊥BE,∴A1D⊥平面BDE.…(3分)
(Ⅱ)解:连B1C.∵A1B1∥CD,∴B1C∥A1D.∵A1D⊥BE,∴B1C⊥BE,
∴∠BB1C=∠CBE,∴Rt△BB1C∽Rt△CBE,
∴
| BC |
| BB1 |
| CE |
| BC |
| 1 |
| 2 |
| 1 |
| 2 |
| B | 2 1 |
| 2 |
取CD中点M,连BM.∵CD=
| 2 |
| ||
| 2 |
过M作MN⊥DE于N,连BN.∵平面CD1⊥平面BD,BM⊥CD,∴BM⊥平面CD1,
∴BN⊥DE,∴∠BNM就是二面角B-DE-C的平面角.…(7分)∵sin∠MDN=
| MN |
| DM |
| CE |
| DE |
| CE2+CD2 |
(
|
| ||
| 2 |
∴MN=
| a | ||
|
| BM |
| MN |
| 5 |
| 5 |
即二面角B-DE-C等于arctan
| 5 |
(Ⅲ)解:∵A1D⊥平面BDE,BN?平面BDE,∴A1D⊥BN.…(10分)
又∵BN⊥DE,∴BN⊥平面A1DE,即BN的长就是点B到平面A1DE的距离.…(11分)
∵BM=
| ||
| 2 |
| a | ||
|
| BM2+MN2 |
| ||
| 5 |
即点B到平面A1DE的距离为
| ||
| 5 |
点评:本题以直平行六面体为载体,考查线面垂直,考查面面角,考查点面距离,关键是利用线面垂直的判定定理,正确表示面面角,线面距离的线段.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

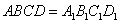 中,
中,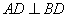 ,
,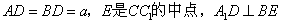
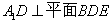 ;
;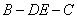 的大小
的大小