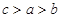题目内容
已知回归直线的斜率的估计值为1.23，样本点的中心为(4,5)，则回归直线方程为
A． | B． |
C． | D． |
C
解析试题分析：设回归直线方程为
∵样本点的中心为（4，5），∴5=1.23×4+a
∴a=0.08∴回归直线方程为故选C．
考点：线性回归方程．
练习册系列答案
相关题目
右图是一容量为
的样本的重量的频率分布直方图，则由图可估计样本重量的中位数为（ ）
A． | B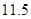． | C． | D． |
某企业为了监控产品质量，从产品流转均匀的生产线上每间隔10分钟抽取一个样本进行检测，这种抽样方法是（ ）
| A．抽签法 | B．随机数表法 | C．系统抽样法 | D．分层抽样法 |
某学校从高二甲、乙两个班中各选6名同掌参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生成绩的众数是 85，乙班学生成绩的平均分为81，则x+y的值为( )
| A．6 | B．7 |
| C．8 | D．9 |
，中位数为
，众数为
，则有（ ）
为了估计某水池中鱼的尾数，先从水池中捕出2000尾鱼，并给每尾鱼做上标记（不影响存活），然后放回水池，经过适当的时间，再从水池中捕出500尾鱼，其中有标记的鱼为40尾，根据上述数据估计该水池中鱼的尾数为（ ）
| A．10000 | B．20000 | C．25000 | D．30000 |
将参加夏令营的600名学生编号为：001，002，……600，采用系统抽样方法抽取一个容量为50的样本，且随机抽得的号码为003．这600名学生分住在三个营区，从001到300在第Ⅰ营区，从301到495住在第Ⅱ营区，从496到600在第Ⅲ营区，三个营区被抽中的人数依次为（ ）
| A．26,16,8, | B．25，17，8 | C．25，16，9 | D．24，17，9 |
某学校有男、女学生各500名，为了解男、女学生在学习兴趣与业余爱好方面是否存在显著差异，拟从全体学生中抽取100名学生进行调查，则宜采用的抽样方法是( )．
| A．抽签法 | B．随机数法 | C．系统抽样法 | D．分层抽样法 |
若回归直线方程的斜率的估计值是1.23，样本点的中心为(4,5)，则回归直线的方程是( )．
A． ＝1.23x＋4 | B．＝1.23x＋5 |
| C．＝1.23x＋0.08 | D．＝0.08x＋1.23 |