Question

已知数列a,b,c为各项都是正数的等差数列，公差为d(d＞0)，在a,b之间和b,c之间共插入m个实数后，所得到的m＋3个数所组成的数列{a_n}是等比数列，其公比为q．
（1）若a＝1,m＝1，求公差d；
（2）若在a,b之间和b,c之间所插入数的个数均为奇数，求所插入的m数的乘积（用a,c,m表示）
（3）求证：q是无理数．

Answer 1

解：（1）由a＝1，且等差数列a,b,c的公差为d，可知b＝1＋d，c＝1＋2d，
①若插入的数在a,b之间，则1＋d＝q²，1＋2d＝q³，消去q可得(1＋2d)²＝(1＋d)³，d＝．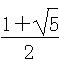
②若插入的数在b,c之间，则1＋d＝q，1＋2d＝q³，消去q可得1＋2d＝(1＋d)³，此方程无正根．
故所求公差d＝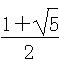
（2）设在a,b之间插入l个数，在b,c之间插入t个数，则l＋t＝m，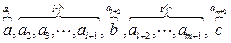
【由等比中项得：】
在等比数列{a_n}中，∵a₁＝a, a_l+2＝b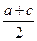＝, a_m+3＝c，a_ka_m+4－k＝a₁a_m+3＝ac(k＝2,3,···,m＋2)，
∴(a₂a₃…a_m+2)²＝(a₂a_m+2)·(a₃a_m+1)···(a_m+2a2)＝(ac)^m+1
又∵q^l+1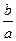＝＞0，q^t+1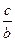＝＞0，l,t都为奇数，∴q可以为正数，也可以为负数．
① 若q为正数，则a₂a₃…a_m+2＝(ac)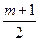，所插入m个数的积为；
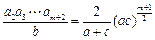②若q为负数，a₂,a₃,…,a_m+2中共有＋1个负数，
当是奇数，即m＝4k－2(k∈N^*)时，所插入m个数的积为；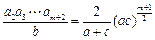
当是偶数，即m＝4k(k∈N^*）时，所插入m个数的积为．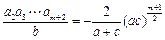
综上所述，当m＝4k－2(k∈N^*)时，所插入m个数的积为；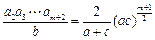
当m＝4k(k∈N^*）时，所插入m个数的积为．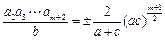
注：可先将a₂,a₃,…,a_m+2用a和q表示，然后再利用条件消去q进行求解．
（3）∵在等比数列{a_n}，由q^l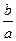+1＝＝，可得q^l+1－1＝，同理可得q^m+2－1＝，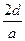
∴q^m+2－1＝2(q^l+1－1)，即2q^l+1－1＝q^m+2 (m≥l)，
反证法：假设q是有理数，
①若q为整数，∵a,b,c是正数，且d＞0，∴|q|＞1，在2q^l+1－q^m+2＝q(2q^l－q^m+1)＝1中，∵2q^l+1－q^m+2是q的倍数，故1也是q的倍数，矛盾．
②若q不是整数，可设q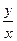＝（其中x,y为互素的整数，x＞1），
则有(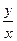)^m+2＝2(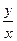)^l+1－1，即y^m+2＝x^m?l+1(2y^l+1－x^l+1)，∵m≥l，可得m－l＋1≥1，
∴y^m+2是x的倍数，即y是x的倍数，矛盾
∴ q是无理数．

解析