题目内容
某工厂有25周岁以上(含2S周岁)工人300名,25周岁以下工人200名为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100),分别加以统计,得到如图所示的频率分布直方图。


(1)求样本中“25周岁以上(含25周岁)组”抽取的人数、日生产量平均数;
(2)若“25周岁以上组”中日平均生产90件及90件以上的称为“生产能手”;“25周岁以下组”中日平均生产不足60件的称为“菜鸟”。从样本中的“生产能手”和”菜鸟”中任意抽取2人,求这2人日平均生产件数之和X的分布列及期望。(“生产能手”日平均生产件数视为95件,“菜鸟”日平均生产件数视为55件)。


(1)求样本中“25周岁以上(含25周岁)组”抽取的人数、日生产量平均数;
(2)若“25周岁以上组”中日平均生产90件及90件以上的称为“生产能手”;“25周岁以下组”中日平均生产不足60件的称为“菜鸟”。从样本中的“生产能手”和”菜鸟”中任意抽取2人,求这2人日平均生产件数之和X的分布列及期望。(“生产能手”日平均生产件数视为95件,“菜鸟”日平均生产件数视为55件)。
(Ⅰ)样本中有 周岁以上组工人
周岁以上组工人 名,平均数为73.5;
名,平均数为73.5;
(2) 的概率分布列:
的概率分布列:
 的期望为158.
的期望为158.
 周岁以上组工人
周岁以上组工人 名,平均数为73.5;
名,平均数为73.5;(2)
 的概率分布列:
的概率分布列: |  |  |  |
 |  |  |  |
 的期望为158.
的期望为158.试题分析:(Ⅰ)分层抽样实质上就是按比例抽样,根据比例即可求得样本中有
 周岁以上组工人的人数;
周岁以上组工人的人数;根据频率分布直方图求平均数的公式为
 ,其中
,其中 为第
为第 组数据的频率,
组数据的频率, 是第
是第 组数据的中间值.由此公式可得样本中“25周岁以上(含25周岁)组”的日生产量平均数.
组数据的中间值.由此公式可得样本中“25周岁以上(含25周岁)组”的日生产量平均数.(2)首先根据频率求出样本中“
 周岁以上组”中的 “生产能手”的人数和 “25周岁以下组”中的“菜鸟”工人的人数. “生产能手”的日平均生产件数为90到100这一组的中间数即95,“菜鸟”的日平均生产件数为50到60这一组的中间数即55,所以随机变量
周岁以上组”中的 “生产能手”的人数和 “25周岁以下组”中的“菜鸟”工人的人数. “生产能手”的日平均生产件数为90到100这一组的中间数即95,“菜鸟”的日平均生产件数为50到60这一组的中间数即55,所以随机变量 取值为190,150,110.由古典概型公式可得其分布列,进而求得其期望.
取值为190,150,110.由古典概型公式可得其分布列,进而求得其期望.试题解析:(Ⅰ)由已知得,样本中有
 周岁以上组工人
周岁以上组工人
 名 4分
名 4分样本中“25周岁以上(含25周岁)组”的日生产量平均数为
 5分
5分(2)由样本中“
 周岁以上组”中日平均生产90件及90件以上的 “生产能手”工人有
周岁以上组”中日平均生产90件及90件以上的 “生产能手”工人有 (人), “25周岁以下组”中日平均生产不足60件的称为“菜鸟”工人有
(人), “25周岁以下组”中日平均生产不足60件的称为“菜鸟”工人有 (人),则这2人日平均生产件数之和
(人),则这2人日平均生产件数之和 取值有180,150,110. 8分
取值有180,150,110. 8分 ,
, ,
,
 的概率分布列:
的概率分布列: |  |  |  |
 |  |  |  |
 的期望
的期望 12分
12分
练习册系列答案
相关题目
 表示编号为
表示编号为 (
(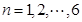 )的同学所得成绩,且前5位同学的成绩如下:70,76,72,70,72.
)的同学所得成绩,且前5位同学的成绩如下:70,76,72,70,72. ,及这6位同学成绩的标准差
,及这6位同学成绩的标准差 ;
; 是指大气中直径小于或等于
是指大气中直径小于或等于 微米的颗粒物,也称为可吸入肺颗粒物.我国
微米的颗粒物,也称为可吸入肺颗粒物.我国 微克/立方米以下空气质量为一级;在
微克/立方米以下空气质量为一级;在 微克/立方米之间空气质量为二级;在
微克/立方米之间空气质量为二级;在 微克/立方米以上空气质量为超标.某试点城市环保局从该市市区
微克/立方米以上空气质量为超标.某试点城市环保局从该市市区 年上半年每天的
年上半年每天的 天的数据作为样本,监测值如下图茎叶图所示(十位为茎,个位为叶).
天的数据作为样本,监测值如下图茎叶图所示(十位为茎,个位为叶).
 天数据,记
天数据,记 表示抽到
表示抽到 天计算)中平均有多少天的空气质量达到一级或二级.
天计算)中平均有多少天的空气质量达到一级或二级.

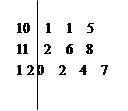
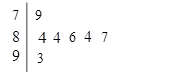
 、
、
 、
、