题目内容
(本小题12分)
已知函数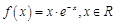
(1)求函数 的单调区间和极值;
的单调区间和极值;
(2)已知 的图象与函数
的图象与函数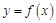 的图象关于直线
的图象关于直线 对称,证明:当
对称,证明:当 时,
时,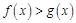 ;
;
(3)如果 且
且 ,证明:
,证明: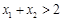
【答案】
(1)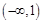 增,
增,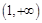 减
减
(2) (3)见解析
【解析】(1)直接求导利用导数大(小)于零求其单调增(减)区间,再根据极值点左正右负是极大值点,左负右正是极小值点。
(2)先根据图像关于x=1对称,可知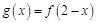 确定出y=g(x)的解析式。然后令
确定出y=g(x)的解析式。然后令 ,再利用导数求h(x)的最小值,证明h(x)min>0即可。
,再利用导数求h(x)的最小值,证明h(x)min>0即可。
(3) 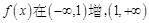 减,且由(2)可知,
减,且由(2)可知, 不可能同时大于1或同时小于1
不可能同时大于1或同时小于1
所以只可能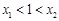 ,
,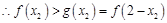 ,又
,又
又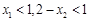 到此问题得以解决。
到此问题得以解决。
解:(1)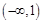 增,
增,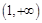 减
减
(2)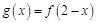
欲证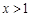 时,
时,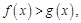 即证
即证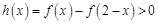
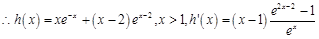
 在
在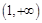 上单调递增
上单调递增 在
在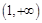 上成立.
上成立.
(3)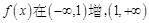 减,且由(2)可知,
减,且由(2)可知, 不可能同时大于1或同时小于1
不可能同时大于1或同时小于1
所以只可能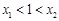 ,
,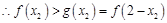
又
又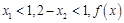 在
在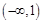 上单调增
上单调增

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
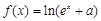 (
( 为常数)是实数集
为常数)是实数集 上的奇函数,函数
上的奇函数,函数 是区间[-1,1]上的减函数.
是区间[-1,1]上的减函数. 在
在 及
及 所在的取值范围上恒成立,求
所在的取值范围上恒成立,求 的取值范围;
的取值范围; 的方程
的方程 的根的个数.
的根的个数. 满足
满足 且
且 .
. 时,不等式:
时,不等式: 恒成立,求实数
恒成立,求实数 的范围.
的范围.
 ,求
,求 的最大值;
的最大值;  ,离心率为
,离心率为 ,且过点
,且过点 ,
,
 (其中
(其中 为参数)所过的定点
为参数)所过的定点 恰在双曲线上,求证:
恰在双曲线上,求证: 。
。 ,直线
,直线 与椭圆C交于不同的两点M,N,以线段MN为直径作圆P。
与椭圆C交于不同的两点M,N,以线段MN为直径作圆P。 直线
直线 ,且直线
,且直线 与曲线
与曲线 相切于点
相切于点 ,求直线
,求直线 的坐标。
的坐标。