题目内容
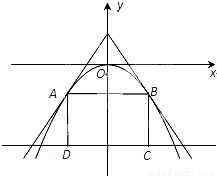
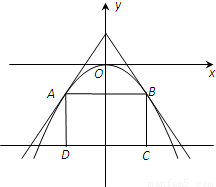
 如图,过点(0,a3)的两直线与抛物线y=-ax2相切于A、B两点,AD、BC垂直于直线y=-8,垂足分别为D、C.
如图,过点(0,a3)的两直线与抛物线y=-ax2相切于A、B两点,AD、BC垂直于直线y=-8,垂足分别为D、C.(1)若a=1,求矩形ABCD面积;
(2)若a∈(0,2),求矩形ABCD面积的最大值.
分析:(1)设出直线与曲线的切点,求出导数后写出切线方程的点斜式,把已知点(0,a3)代入切线方程,求出两个切点的横坐标,从而得到矩形ABCD的长和宽,则面积即可用含a的代数式表示,把a=1代入后可求矩形面积;
(2)对(1)中求出的面积表达式求导,利用导数判出函数在(0,2)上的单调性,求出函数在(0,2)上的极值,则最值可求.
(2)对(1)中求出的面积表达式求导,利用导数判出函数在(0,2)上的单调性,求出函数在(0,2)上的极值,则最值可求.
解答:解:(1)设切点为(x0,y0),则y0=-ax02,
因为y'=-2ax,所以切线方程为y-y0=-2ax0(x-x0),即y+ax02=-2ax0(x-x0),
因为切线过点(0,a3),所以a3+ax02=-2ax0(0-x0),即a3=ax02,于是x0=±a.
将x0=±a代入y0=-ax02得y0=-a3.
所以AB=2a,BC=8-a3,所以矩形ABCD面积为S=16a-2a4,
当a=1时,矩形ABCD的面积S=16×1-2×14=14;
(2)由(1)得:矩形ABCD面积为S=16a-2a4(0<a<2),
则S'=16-8a3=8(2-a3).
所以当0<a<
时,S'>0;当
<a<2时,S'<0;
故当a=
时,S有最大值为S=16×
-2×(
)4=12
.
因为y'=-2ax,所以切线方程为y-y0=-2ax0(x-x0),即y+ax02=-2ax0(x-x0),
因为切线过点(0,a3),所以a3+ax02=-2ax0(0-x0),即a3=ax02,于是x0=±a.
将x0=±a代入y0=-ax02得y0=-a3.
所以AB=2a,BC=8-a3,所以矩形ABCD面积为S=16a-2a4,
当a=1时,矩形ABCD的面积S=16×1-2×14=14;
(2)由(1)得:矩形ABCD面积为S=16a-2a4(0<a<2),
则S'=16-8a3=8(2-a3).
所以当0<a<
| 3 | 2 |
| 3 | 2 |
故当a=
| 3 | 2 |
| 3 | 2 |
| 3 | 2 |
| 3 | 2 |
点评:本题考查利用导数求曲线上过某点的切线方程,会利用导数研究函数的单调区间以及根据函数的增减性得到函数的极值,是中档题.

练习册系列答案
相关题目
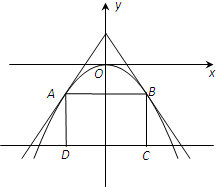 如图,过点(0,a3)(0<a<2)的两直线与抛物线y=-ax2相切于A,B两点,AD,BC垂直于直线y=-8,垂足分别为D、C,求矩形ABCD面积的最大值.
如图,过点(0,a3)(0<a<2)的两直线与抛物线y=-ax2相切于A,B两点,AD,BC垂直于直线y=-8,垂足分别为D、C,求矩形ABCD面积的最大值.