题目内容
已知椭圆 的两个焦点坐标分别是
的两个焦点坐标分别是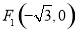 、
、 ,并且经过点
,并且经过点 .
.
(1)求椭圆 的方程;
的方程;
(2)若直线 与圆
与圆 :
: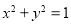 相切,并与椭圆
相切,并与椭圆 交于不同的两点
交于不同的两点 、
、 .当
.当 ,且满足
,且满足 时,求
时,求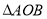 面积
面积 的取值范围.
的取值范围.
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
题目内容
已知椭圆 的两个焦点坐标分别是
的两个焦点坐标分别是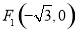 、
、 ,并且经过点
,并且经过点 .
.
(1)求椭圆 的方程;
的方程;
(2)若直线 与圆
与圆 :
: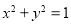 相切,并与椭圆
相切,并与椭圆 交于不同的两点
交于不同的两点 、
、 .当
.当 ,且满足
,且满足 时,求
时,求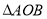 面积
面积 的取值范围.
的取值范围.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案