题目内容
已知函数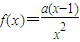 ,其中a>0.
,其中a>0.(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若直线x-y-1=0是曲线y=f(x)的切线,求实数a的值;
(Ⅲ)设g(x)=xlnx-x2f(x),求g(x)在区间[1,e]上的最大值.(其中e为自然对数的底数)
【答案】分析:(Ⅰ)先求导函数,直接让导函数大于0求出增区间,导函数小于0求出减区间即可;
(Ⅱ)直接利用切线的斜率即为切点处的导数值以及切点是直线与曲线的共同点联立方程即可求实数a的值;
(Ⅲ)先求出g(x)的导函数,分情况讨论出函数在在区间[1,e]上的单调性,进而求得其在区间[1,e]上的最大值.
解答:解:(Ⅰ)′因为函数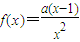 ,
,
∴f′(x)=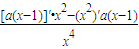 =
=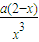
f′(x)>0⇒0<x<2,f′(x)<0⇒x<0,x>2,
故函数在(0,2)上递增,在(-∞,0)和(2,+∞)上递减.
(Ⅱ)设切点为(x,y),
由切线斜率k=1=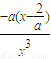 ,⇒x3=-ax+2,①
,⇒x3=-ax+2,①
由x-y-1=x-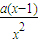 -1=0⇒(x2-a)(x-1)=0⇒x=1,x=±
-1=0⇒(x2-a)(x-1)=0⇒x=1,x=±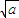 .
.
把x=1代入①得a=1,
把x=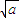 代入①得a=1,
代入①得a=1,
把x=-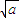 代入①得a=-1,
代入①得a=-1,
∵a>0.
故所求实数a的值为1
(Ⅲ)∵g(x)=xlnx-x2f(x)=xlnx-a(x-1),
∴g′(x)=lnx+1-a,且g′(1)=1-a,g′(e)=2-a.
当a<1时,g′(1)>0,g′(e)>0,故g(x)在区间[1,e]上递增,其最大值为g(e)=a+e(1-a);
当1<a<2时,g′(1)<0,g′(e)>0,故g(x)在区间[1,e]上先减后增且g(1)=0,g(e)>0.所以g(x)在区间[1,e]上的最大值为g(e)=a+e(1-a);
当a>2时,g′(1),0,g′(e)<0,g(x)在区间[1,e]上递减,故最大值为g(1)=0.
点评:本题主要考查利用导数求闭区间上函数的最值以及利用导数研究函数的单调性,是高考的常考题型.
(Ⅱ)直接利用切线的斜率即为切点处的导数值以及切点是直线与曲线的共同点联立方程即可求实数a的值;
(Ⅲ)先求出g(x)的导函数,分情况讨论出函数在在区间[1,e]上的单调性,进而求得其在区间[1,e]上的最大值.
解答:解:(Ⅰ)′因为函数
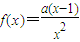 ,
,∴f′(x)=
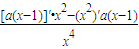 =
=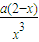
f′(x)>0⇒0<x<2,f′(x)<0⇒x<0,x>2,
故函数在(0,2)上递增,在(-∞,0)和(2,+∞)上递减.
(Ⅱ)设切点为(x,y),
由切线斜率k=1=
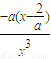 ,⇒x3=-ax+2,①
,⇒x3=-ax+2,①由x-y-1=x-
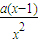 -1=0⇒(x2-a)(x-1)=0⇒x=1,x=±
-1=0⇒(x2-a)(x-1)=0⇒x=1,x=±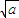 .
.把x=1代入①得a=1,
把x=
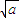 代入①得a=1,
代入①得a=1,把x=-
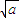 代入①得a=-1,
代入①得a=-1,∵a>0.
故所求实数a的值为1
(Ⅲ)∵g(x)=xlnx-x2f(x)=xlnx-a(x-1),
∴g′(x)=lnx+1-a,且g′(1)=1-a,g′(e)=2-a.
当a<1时,g′(1)>0,g′(e)>0,故g(x)在区间[1,e]上递增,其最大值为g(e)=a+e(1-a);
当1<a<2时,g′(1)<0,g′(e)>0,故g(x)在区间[1,e]上先减后增且g(1)=0,g(e)>0.所以g(x)在区间[1,e]上的最大值为g(e)=a+e(1-a);
当a>2时,g′(1),0,g′(e)<0,g(x)在区间[1,e]上递减,故最大值为g(1)=0.
点评:本题主要考查利用导数求闭区间上函数的最值以及利用导数研究函数的单调性,是高考的常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,其中a>0.
,其中a>0. ,其中a>0.
,其中a>0.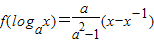 ,其中a>0且a≠1.
,其中a>0且a≠1.