题目内容
设椭圆
+
=1(a>b>0)的两焦点为F1、F2,若椭圆上存在一点Q,使∠F1QF2=120°,椭圆离心率e的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
A.
| B.
| C.0<e≤
| D.
|
椭圆的焦点在x轴,设椭圆的上顶点为A,
∵椭圆上存在一点Q,∠F1QF2=120°,
∴∠F1AO≥60°,
∴tan∠F1AO=
≥
,
∴
≤
?
=
≤
,
∴
≥
,
∴e=
≥
,又e<1.
∴
≤e<1.
故选A.
∵椭圆上存在一点Q,∠F1QF2=120°,
∴∠F1AO≥60°,
∴tan∠F1AO=
| c |
| b |
| 3 |
∴
| b2 |
| c2 |
| 1 |
| 3 |
| b2 |
| c2 |
| a2-c2 |
| c2 |
| 1 |
| 3 |
∴
| c2 |
| a2 |
| 3 |
| 4 |
∴e=
| c |
| a |
| ||
| 2 |
∴
| ||
| 2 |
故选A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
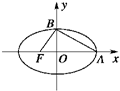
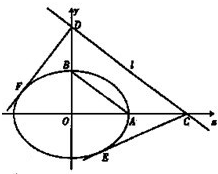
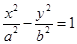 (a>b>0)的一个焦点为
(a>b>0)的一个焦点为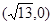 ,离心率为
,离心率为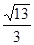 .
.