题目内容
(12分)
已知定点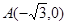 ,B是圆
,B是圆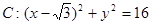 (C为圆心)上的动点,AB的垂直平分线与BC交于点E.
(C为圆心)上的动点,AB的垂直平分线与BC交于点E.
(1)求动点E的轨迹方程;
(2)设直线 与E的轨迹交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求:
与E的轨迹交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求: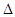 OPQ面积的最大值及此时直线
OPQ面积的最大值及此时直线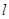 的方程.
的方程.
【答案】
解:(1)由题知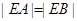
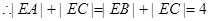 (2分)
(2分)
又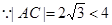
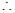 点E的轨迹是以A,C为焦点,长轴长为4的椭圆,
点E的轨迹是以A,C为焦点,长轴长为4的椭圆,
 E的轨迹方程为
E的轨迹方程为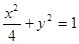 (4分)
(4分)
(2)设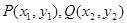 ,PQ的中点为
,PQ的中点为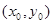
将直线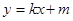 与
与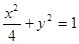 联立得
联立得
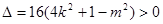 ,即
,即 ①
①
又
依题意有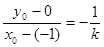 ,整理得
,整理得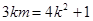 ② (6分)
② (6分)
由①②可得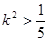 ,
,

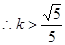 (7分)
(7分)
设O到直线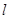 的距离为
的距离为 ,则
,则
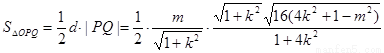
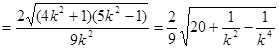 (10分)
(10分)
当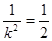 时,
时, 的面积取最大值1,此时
的面积取最大值1,此时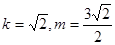 ,
,
 直线方程为
直线方程为
【解析】略

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
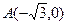 ,B是圆
,B是圆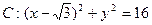 (C为圆心)上的动点,AB的垂直平分线与BC交于点E.
(C为圆心)上的动点,AB的垂直平分线与BC交于点E.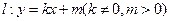 与E的轨迹交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求:
与E的轨迹交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求: OPQ面积的最大值及此时直线
OPQ面积的最大值及此时直线 的方程.
的方程.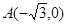 ,B是圆
,B是圆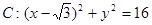 (C为圆心)上的动点,AB的垂直平分线与BC交于点E。
(C为圆心)上的动点,AB的垂直平分线与BC交于点E。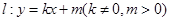 与E的轨迹交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求:
与E的轨迹交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求: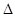 OPQ面积的最大值及此时直线
OPQ面积的最大值及此时直线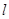 的方程。
的方程。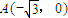 ,B是圆
,B是圆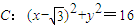 (C为圆心)上的动点,AB的垂直平分线与BC交于点E.
(C为圆心)上的动点,AB的垂直平分线与BC交于点E. ,B是圆
,B是圆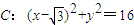 (C为圆心)上的动点,AB的垂直平分线与BC交于点E.
(C为圆心)上的动点,AB的垂直平分线与BC交于点E.