题目内容
(本小题满分12分)已知各项都不相等的等差数列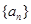 的前6项和为60,且
的前6项和为60,且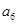 为
为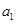 和
和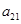 的等比中项.
的等比中项.
( I ) 求数列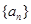 的通项公式;
的通项公式;
(II) 若数列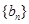 满足
满足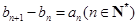 ,且
,且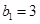 ,求数列
,求数列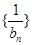 的前
的前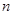 项和
项和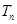 .
.
(Ⅰ)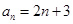 ;(Ⅱ)
;(Ⅱ) 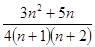 。
。
解析试题分析:(Ⅰ)设等差数列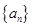 的公差为
的公差为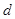 (
(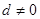 ),则
),则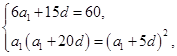 …2
…2
解得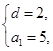 ……4分∴
……4分∴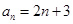 . ………………5分
. ………………5分
(Ⅱ)由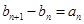 ,∴
,∴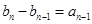
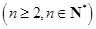 ,……………6分
,……………6分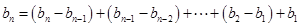
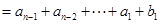
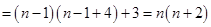 .
.
∴
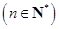 …8分∴
…8分∴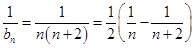 …10分
…10分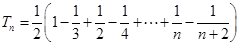
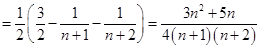 …12分
…12分
考点:等差数列的简单性质;等比中项;通项公式的求法;数列求和。
点评:若已知递推公式为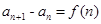 的形式求通项公式常用累加法。
的形式求通项公式常用累加法。
注:①若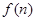 是关于n的一次函数,累加后可转化为等差数列求和;
是关于n的一次函数,累加后可转化为等差数列求和;
②若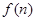 是关于n的二次函数,累加后可分组求和;
是关于n的二次函数,累加后可分组求和;
③若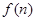 是关于n的指数函数,累加后可转化为等比数列求和;
是关于n的指数函数,累加后可转化为等比数列求和;
④若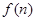 是关于n的分式函数,累加后可裂项求和。
是关于n的分式函数,累加后可裂项求和。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
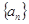 的首项为1,其前n项和为
的首项为1,其前n项和为 ,
,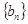 是公比为正整数的等比数列,其首项为3,前n项和为
是公比为正整数的等比数列,其首项为3,前n项和为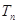 . 若
. 若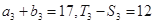 .
.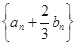 的前n项和
的前n项和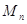 .(5分)
.(5分) ,且
,且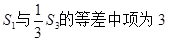
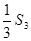 , 求和Tn=a1b1+a2b2+…+anbn
, 求和Tn=a1b1+a2b2+…+anbn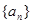 的前n项和为
的前n项和为 ,且
,且 ,(
,( =1,2,3…)
=1,2,3…)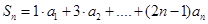 ,求
,求 中,
中, ,且
,且 、
、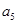 、
、 成等比数列.
成等比数列. ,求数列
,求数列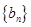 的前
的前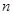 项的和
项的和 .
. 为等差数列,且
为等差数列,且 ,
, .
. ,求证:数列
,求证:数列 是等比数列.
是等比数列.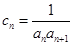 ,求数列
,求数列 的前
的前 项和
项和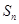 .
. 是公差不为零的等差数列,
是公差不为零的等差数列,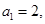 且
且 成等比数列
成等比数列 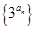 的前
的前 项和
项和 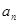 }中,
}中,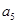 =162,公比q=3,前n项和
=162,公比q=3,前n项和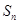 =242,求首项
=242,求首项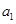 和项数n的值.
和项数n的值.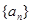 的前n项和,
的前n项和,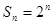 ,求
,求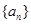 的前
的前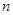 项和为
项和为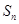 ,且
,且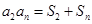 对一切正整数
对一切正整数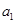 ,
,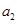 的值;
的值;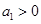 ,数列
,数列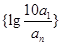 的前
的前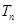 ,当
,当