题目内容
已知正三棱锥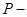
ABC,点P,A,B,C都在半径为
的球面上,若PA,PB,PC两两互相垂直,则球心到截面ABC的距离为____________.
解析试题分析：因为正三棱锥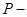ABC,PA,PB,PC两两互相垂直,所以我们可以把正三棱锥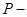ABC,放到正方体中，P、A、B、C为正方体的顶点，则正三棱锥
ABC的外接球的球心为正方体体对角线的交点，在正方体ABCD-A1B1C1D1中，面A1BD和面CB1D1把体对角线三等分，所以球心到截面ABC的距离为.
考点：正三棱锥的结构特征、几何体的外接球的有关问题.
练习册系列答案
相关题目
的底面是矩形，顶点
在底面
内的射影是矩形
垂直于主视图投影平面）．则四棱锥的
若将圆锥倒置后，圆锥内水面高为
cm,则侧面展开图所在扇形的圆心角=______.