ЬтФПФкШн
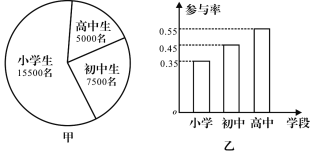
ЁОЬтФПЁПНЛЧПЯеЪЧГЕжїБиаыЮЊЛњЖЏГЕЙКТђЕФЯежжЃЌЪЕааЕФЪЧЗбТЪИЁЖЏЛњжЦЃЌБЃЗбгыЩЯвЛФъЖШГЕСОЗЂЩњЕРТЗНЛЭЈЪТЙЪЕФЧщПіЯрСЊЯЕ.УПФъНЛЧПЯезюжеБЃЯеЗбМЦЫуЗНЗЈЪЧЃКНЛЧПЯезюжеБЃЯеЗб![]() ЃЌЦфжаaЮЊНЛЧПЯеЛљДЁБЃЯеЗбЃЌAЮЊгыЕРТЗНЛЭЈЪТЙЪЯрСЊЯЕЕФИЁЖЏБШТЪЃЌЭЌЪБТњзуЖрИіИЁЖЏвђЫиЕФЃЌАДееЯђЩЯИЁЖЏЛђепЯђЯТИЁЖЏБШТЪЕФИпепМЦЫу.АДееЮвЙњЁЖЛњЖЏГЕНЛЭЈЪТЙЪд№ШЮЧПжЦБЃЯеЛљДЁЗбТЪБэЁЗЕФЙцЖЈЃКЦеЭЈ6зљвдЯТЫНМвГЕЕФНЛЧПЯеЛљДЁБЃЯеЗб
ЃЌЦфжаaЮЊНЛЧПЯеЛљДЁБЃЯеЗбЃЌAЮЊгыЕРТЗНЛЭЈЪТЙЪЯрСЊЯЕЕФИЁЖЏБШТЪЃЌЭЌЪБТњзуЖрИіИЁЖЏвђЫиЕФЃЌАДееЯђЩЯИЁЖЏЛђепЯђЯТИЁЖЏБШТЪЕФИпепМЦЫу.АДееЮвЙњЁЖЛњЖЏГЕНЛЭЈЪТЙЪд№ШЮЧПжЦБЃЯеЛљДЁЗбТЪБэЁЗЕФЙцЖЈЃКЦеЭЈ6зљвдЯТЫНМвГЕЕФНЛЧПЯеЛљДЁБЃЯеЗб![]() ЮЊ950дЊЃЌНЛЧПЯеЗбТЪИЁЖЏвђЫиМАБШТЪШчЯТБэЃК
ЮЊ950дЊЃЌНЛЧПЯеЗбТЪИЁЖЏвђЫиМАБШТЪШчЯТБэЃК
НЛЧПЯеИЁЖЏвђЫиКЭИЁЖЏЗбТЪБШТЪБэ | ||
РраЭ | ИЁЖЏвђЫи | ИЁЖЏБШТЪ |
| ЩЯвЛИіФъЖШЮДЗЂЩњгад№ШЮЕРТЗНЛЭЈЪТЙЪ |
|
| ЩЯСНИіФъЖШЮДЗЂЩњгад№ШЮЕРТЗНЛЭЈЪТЙЪ |
|
| ЩЯШ§ИіМАвдЩЯФъЖШЮДЗЂЩњгад№ШЮЕРТЗНЛЭЈЪТЙЪ |
|
| ЩЯвЛИіФъЖШЗЂЩњвЛДЮгад№ШЮВЛЩцМАЫРЭіЕФЕРТЗНЛЭЈЪТЙЪ |
|
| ЩЯвЛИіФъЖШЗЂЩњСНДЮМАвдЩЯгад№ШЮЕРТЗНЛЭЈЪТЙЪ |
|
| ЩЯвЛИіФъЖШЗЂЩњгад№ШЮЕРТЗНЛЭЈЫРЭіЪТЙЪ |
|
ФГЛњЙЙЮЊСЫбаОПФГвЛЦЗХЦЦеЭЈ6зљвдЯТЫНМвГЕЕФЭЖБЃЧщПіЃЌЫцЛњГщШЁСЫ100СОГЕСфвбТњШ§ФъЕФИУЦЗХЦЭЌаЭКХЫНМвГЕЕФЯТвЛФъајБЃЪБЕФЧщПіЃЌЭГМЦНсЙћШчЯТБэЃК
РраЭ |
|
|
|
|
|
|
Ъ§СП | 25 | 10 | 10 | 25 | 20 | 10 |
вдет100СОИУЦЗХЦГЕЕФЭЖБЃРраЭЕФЦЕТЪДњЬцвЛСОГЕЭЖБЃРраЭЕФИХТЪЃЌЭъГЩЯТСаЮЪЬт.
ЃЈ1ЃЉМЧXЮЊвЛСОИУЦЗХЦГЕдкЕкЫФФъајБЃЪБЕФЗбгУЃЌЧѓXЕФЗжВМСагыЪ§бЇЦкЭћЃЈЪ§бЇЦкЭћжЕБЃСєЕНИіЮЛЪ§зжЃЉЃЛ
ЃЈ2ЃЉФГЖўЪжГЕЯњЪлЩЬзЈУХЯњЪлетвЛЦЗХЦЕФЖўЪжГЕЃЌЧвНЋОЯњЩЬЙКГЕКѓЯТвЛФъЕФНЛЧПЯезюжеБЃЯеЗбИпгкНЛЧПЯеЛљДЁБЃЯеЗб![]() ЕФГЕСОМЧЮЊЪТЙЪГЕЃЌМйЩшЙКНјвЛСОЪТЙЪГЕПїЫ№3000дЊЃЌЙКНјвЛСОЗЧЪТЙЪГЕгЏРћ5000дЊ.
ЕФГЕСОМЧЮЊЪТЙЪГЕЃЌМйЩшЙКНјвЛСОЪТЙЪГЕПїЫ№3000дЊЃЌЙКНјвЛСОЗЧЪТЙЪГЕгЏРћ5000дЊ.
ЂйШєИУЯњЪлЩЬЙКНјШ§СОЃЈГЕСфвбТњШ§ФъЃЉИУЦЗХЦЖўЪжГЕЃЌЧѓетШ§СОГЕжажСЩйгавЛСОЪЧЪТЙЪГЕЕФИХТЪЃЛ
ЂкШєИУЯњЪлЩЬвЛДЮЙКНј100СОЃЈГЕСфвбТњШ§ФъЃЉИУЦЗХЦЖўЪжГЕЃЌЧѓЫћЛёЕУРћШѓЕФЦкЭћ.
ЁОД№АИЁПЃЈ1ЃЉЗжВМСаМћНтЮіЃЛ926ЃЛЃЈ2ЃЉЂй![]() ЃЛЂк26ЭђдЊ.
ЃЛЂк26ЭђдЊ.
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвтПЩжЊXЕФЫљгаПЩФмШЁжЕЮЊ0.9aЃЌ0.8aЃЌ0.7aЃЌaЃЌ1.1aЃЌ1.3aЃЌЃЌгЩЭГМЦЪ§ОнЗжБ№ЧѓГіЯргІЕФИХТЪЃЌгЩДЫЧѓГіXЕФЗжВМСаКЭЪ§бЇЦкЭћЃЛ
ЃЈ2ЃЉЂйгЩЭГМЦЪ§ОнПЩжЊШЮвтвЛСОИУЦЗХЦГЕСфвбТњШ§ФъЕФЖўЪжГЕЮЊЪТЙЪГЕЕФИХТЪ![]() ЃЌгЩДЫФмЧѓГіШ§СОГЕжажСЩйгавЛСОЪЧЪТЙЪГЕЕФИХТЪЃЛ
ЃЌгЩДЫФмЧѓГіШ§СОГЕжажСЩйгавЛСОЪЧЪТЙЪГЕЕФИХТЪЃЛ
ЂкЩшИУЯњЪлЩЬЙКНјвЛСОЖўЪжГЕЛёЕУЕФРћШѓЮЊYЃЌдђYЕФЫљгаПЩФмШЁжЕЮЊ![]() ЃЌ5000.гЩДЫФмЧѓГіYЕФЗжВМСаКЭЪ§бЇЦкЭћЃЌДгЖјПЩЕУИУЯњЪлЩЬвЛДЮЙКНј100СОЃЈГЕСфвбТњШ§ФъЃЉИУЦЗХЦЖўЪжГЕЛёЕУРћШѓЕФЦкЭћ
ЃЌ5000.гЩДЫФмЧѓГіYЕФЗжВМСаКЭЪ§бЇЦкЭћЃЌДгЖјПЩЕУИУЯњЪлЩЬвЛДЮЙКНј100СОЃЈГЕСфвбТњШ§ФъЃЉИУЦЗХЦЖўЪжГЕЛёЕУРћШѓЕФЦкЭћ
ЃЈ1ЃЉгЩЬтвтПЩжЊXЕФЫљгаПЩФмШЁжЕЮЊ0.9aЃЌ0.8aЃЌ0.7aЃЌaЃЌ1.1aЃЌ1.3aЃЌ
гЩЭГМЦЪ§ОнПЩжЊЃК
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЫљвдXЕФЗжВМСаЮЊЃК
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ёр![]() .
.
ЃЈ2ЃЉЂйгЩЭГМЦЪ§ОнПЩжЊШЮвтвЛСОИУЦЗХЦГЕСфвбТњШ§ФъЕФЖўЪжГЕЮЊЪТЙЪГЕЕФИХТЪ![]() ЃЌ
ЃЌ
дђШ§СОГЕжажСЩйгавЛСОЪТЙЪГЕЕФИХТЪЮЊ![]() ЃЛ
ЃЛ
ЂкЩшИУЯњЪлЩЬЙКНјвЛСОЖўЪжГЕЛёЕУЕФРћШѓЮЊYЃЌ
дђYЕФЫљгаПЩФмШЁжЕЮЊ![]() ЃЌ5000.
ЃЌ5000.
ЫљвдYЕФЗжВМСаЮЊЃК
Y |
| 5000 |
|
|
|
Ыљвд![]() .
.
ЫљвдИУЯњЪлЩЬвЛДЮЙКНј100СОЃЈГЕСфвбТњШ§ФъЃЉИУЦЗХЦЕФЖўЪжГЕЛёЕУРћШѓЕФЦкЭћЮЊ
![]() ЭђдЊ.
ЭђдЊ.