题目内容
建造一个容积为18m3, 深为2m的长方形无盖水池,如果池底和池壁每m2的造价分别为200元和150元,如何设计水池的长和宽能使得水池的造价最低?最低造价是多少?
当水池的底面是3米的正方形时,水池的造价最低,最低造价为5400元.
容积为18m3, 深为2m的长方体,其底面积为9 ,设水池的底边长为
,设水池的底边长为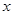 米,则宽为
米,则宽为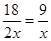 米,水池的造价分为池底和池壁两部分,设为
米,水池的造价分为池底和池壁两部分,设为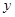 元,则
元,则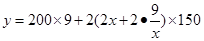
由不等式求出最值及此时对应的底边长.
设水池的底边长为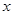 米,则宽为
米,则宽为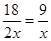 米,水池的造价为
米,水池的造价为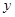 元,那么
元,那么
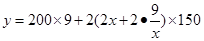 (
(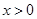 )
)
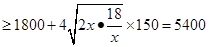
当且仅当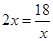 时等号成立,此时长为
时等号成立,此时长为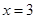 ,宽为3米.
,宽为3米.
所以,当水池的底面是3米的正方形时,水池的造价最低,最低造价为5400元.
 ,设水池的底边长为
,设水池的底边长为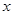 米,则宽为
米,则宽为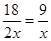 米,水池的造价分为池底和池壁两部分,设为
米,水池的造价分为池底和池壁两部分,设为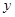 元,则
元,则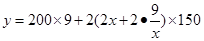
由不等式求出最值及此时对应的底边长.
设水池的底边长为
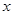 米,则宽为
米,则宽为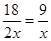 米,水池的造价为
米,水池的造价为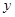 元,那么
元,那么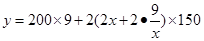 (
(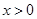 )
)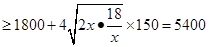
当且仅当
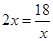 时等号成立,此时长为
时等号成立,此时长为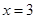 ,宽为3米.
,宽为3米.所以,当水池的底面是3米的正方形时,水池的造价最低,最低造价为5400元.

练习册系列答案
相关题目
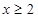 时,
时,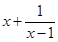 的最小值是
的最小值是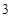 ;
;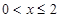 时,
时,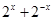 存在最大值;
存在最大值;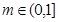 ,则函数
,则函数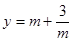 的最小值为
的最小值为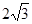 ;
;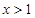 时,
时,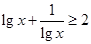 .
.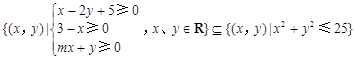 ,则m的最大值是( )
,则m的最大值是( )


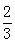
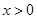 ,
,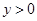 ,
,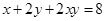 ,则
,则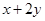 的最小值是( )
的最小值是( )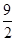
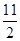
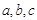 满足:
满足: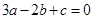 ,则
,则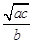 的最大值为 .
的最大值为 .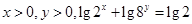 ,则
,则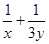 的最小值是( )
的最小值是( )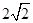
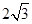
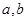 满足
满足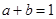 ,则( )
,则( )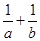 有最大值4
有最大值4 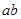 有最小值
有最小值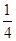
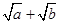 有最大值
有最大值
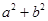 有最小值
有最小值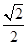
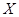 的分布列如下表, 则
的分布列如下表, 则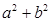 的最小值为 .
的最小值为 .