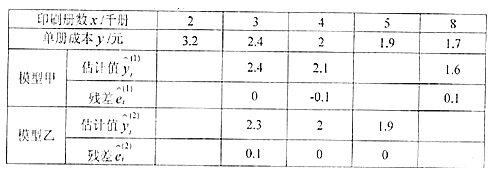
题目内容
【题目】已知过原点的动直线l与圆C1:x2+y2﹣6x+5=0相交于不同的两点A,B.
(1)求圆C1的圆心坐标;
(2)求线段AB 的中点M的轨迹C的方程;
(3)是否存在实数 k,使得直线L:y=k(x﹣4)与曲线 C只有一个交点?若存在,求出k的取值范围;若不存在,说明理由.
【答案】
(1)解:∵圆C1:x2+y2﹣6x+5=0,
整理,得其标准方程为:(x﹣3)2+y2=4,
∴圆C1的圆心坐标为(3,0)
(2)解:设当直线l的方程为y=kx、A(x1,y1)、B(x2,y2),
联立方程组 ![]() ,
,
消去y可得:(1+k2)x2﹣6x+5=0,
由△=36﹣4(1+k2)×5>0,可得k2< ![]()
由韦达定理,可得x1+x2= ![]() ,
,
∴线段AB的中点M的轨迹C的参数方程为 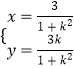 ,其中﹣
,其中﹣ ![]() <k<
<k< ![]() ,
,
∴线段AB的中点M的轨迹C的方程为:(x﹣ ![]() )2+y2=
)2+y2= ![]() ,其中
,其中 ![]() <x≤3
<x≤3
(3)解:结论:当k∈(﹣ ![]() ,
, ![]() )∪{﹣
)∪{﹣ ![]() ,
, ![]() }时,直线L:y=k(x﹣4)与曲线C只有一个交点.
}时,直线L:y=k(x﹣4)与曲线C只有一个交点.
理由如下:
联立方程组 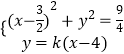 ,
,
消去y,可得:(1+k2)x2﹣(3+8k2)x+16k2=0,
令△=(3+8k2)2﹣4(1+k2)16k2=0,解得k=± ![]() ,
,
又∵轨迹C的端点( ![]() ,±
,± ![]() )与点(4,0)决定的直线斜率为±
)与点(4,0)决定的直线斜率为± ![]() ,
,
∴当直线L:y=k(x﹣4)与曲线C只有一个交点时,
k的取值范围为(﹣ ![]() ,
, ![]() )∪{﹣
)∪{﹣ ![]() ,
, ![]() }
}
【解析】(1)通过将圆C1的一般式方程化为标准方程即得结论;(2)设当直线l的方程为y=kx,通过联立直线l与圆C1的程,利用根的判别式大于0、韦达定理、中点坐标公式及参数方程与普通方程的相互转化,计算即得结论;(3)通过联立直线L与圆C1的方程,利用根的判别式△=0及轨迹C的端点与点(4,0)决定的直线斜率,即得结论.

【题目】某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
(Ⅰ)求图中a的值;
(Ⅱ)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(Ⅲ)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?