题目内容
已知函数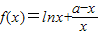 ,其中a为大于零的常数.
,其中a为大于零的常数.(I)若曲线y=f(x)在点(1,f(1))处的切线与直线y=1-2x平行,求a的值;
(II)求函数f(x)在区间[1,2]上的最小值.
【答案】分析:(I)先由所给函数的表达式,求导数fˊ(x),再根据导数的几何意义求出切线的斜率,最后由平行直线的斜率相等方程求a的值即可;
(II)对参数a进行分类,先研究f(x)在[1,2]上的单调性,利用导数求解f(x)在[1,2]上的最小值问题即可,故只要先求出函数的极值,比较极值和端点处的函数值的大小,最后确定出最小值即得.
解答:解: (x>0)(.4分)
(x>0)(.4分)
(I)因为曲线y=f(x)在点(1,f(1))处的切线与直线y=1-2x平行,
所以f'(1)=-2,即1-a=-2,解得a=3.(6分)
(II)当0<a≤1时,f'(x)>0在(1,2)上恒成立,
这时f(x)在[1,2]上为增函数∴f(x)min=f(1)=a-1.(8分)
当1<a<2时,由f'(x)=0得,x=a∈(1,2)∵对于x∈(1,a)有f'(x)<0,f(x)在[1,a]上为减函数,
对于x∈(a,2)有f'(x)>0,f(x)在[a,2]上为增函数,∴f(x)min=f(a)=lna.(11分)
当a≥2时,f'(x)<0在(1,2)上恒成立,
这时f(x)在[1,2]上为减函数,∴ .
.
综上,f(x)在[1,2]上的最小值为
①当0<a≤1时,f(x)min=a-1,
②当1<a<2时,f(x)min=lna,
③当a≥2时, (13分)
(13分)
点评:本小题主要考查利用导数研究曲线上某点切线方程、函数的最值及其几何意义、两条直线平行的判定等基础知识,考查运算求解能力,考查分类讲座思想、化归与转化思想.属于基础题.
(II)对参数a进行分类,先研究f(x)在[1,2]上的单调性,利用导数求解f(x)在[1,2]上的最小值问题即可,故只要先求出函数的极值,比较极值和端点处的函数值的大小,最后确定出最小值即得.
解答:解:
 (x>0)(.4分)
(x>0)(.4分)(I)因为曲线y=f(x)在点(1,f(1))处的切线与直线y=1-2x平行,
所以f'(1)=-2,即1-a=-2,解得a=3.(6分)
(II)当0<a≤1时,f'(x)>0在(1,2)上恒成立,
这时f(x)在[1,2]上为增函数∴f(x)min=f(1)=a-1.(8分)
当1<a<2时,由f'(x)=0得,x=a∈(1,2)∵对于x∈(1,a)有f'(x)<0,f(x)在[1,a]上为减函数,
对于x∈(a,2)有f'(x)>0,f(x)在[a,2]上为增函数,∴f(x)min=f(a)=lna.(11分)
当a≥2时,f'(x)<0在(1,2)上恒成立,
这时f(x)在[1,2]上为减函数,∴
 .
.综上,f(x)在[1,2]上的最小值为
①当0<a≤1时,f(x)min=a-1,
②当1<a<2时,f(x)min=lna,
③当a≥2时,
 (13分)
(13分)点评:本小题主要考查利用导数研究曲线上某点切线方程、函数的最值及其几何意义、两条直线平行的判定等基础知识,考查运算求解能力,考查分类讲座思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
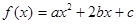 ,其中a≥b>c,a+b+c=0.
,其中a≥b>c,a+b+c=0.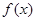 有两个零点;
有两个零点;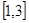 上的最小值为1,最大值为13,求a、b、c的值.
上的最小值为1,最大值为13,求a、b、c的值.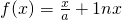 ,其中a为常数,e为自然对数的底数.
,其中a为常数,e为自然对数的底数. ,其中a为常数,e为自然对数的底数.
,其中a为常数,e为自然对数的底数.