题目内容

已知z、w、x为复数，且x=（1+3i）•z，w=
z
2+i
且|w|=5
2
．
（1）若w为大于0的实数，求复数x．
（2）若x为纯虚数，求复数w．
（1）∵x=（1+3i）•z，∴z=
x
1+3i
．
若w为大于0的实数，
∵w=
z
2+i
=
x
(1+3i)(2+i)
=
x
-1+7i
，|w|=5
2
，
则有 5
2
=
x
-1+7i
，∴x=-5
2
+35
2
i．
（2）若x为纯虚数，设x=bi，b≠0．
由（1）可得 |
x
-1+7i
|=|
bi
-1+7i
|=5
2
，∴b=±50．
∴w=
x
-1+7i
=
50i
-1+7i
=7-i，或w=
x
-1+7i
=
-50i
-1+7i
=-7+i．
练习册系列答案
相关题目
下面是关于复数z=-
1
2
+
3
2
i的四个命题，其中真命题为（　　）
A．z的虚部为
3
2
i		B．z为纯虚数
C．|z|=2D．z2=
.
z
（Ⅰ）复数z满足（1+2i）z+（3-10i）
.
z
=4-34i，求z；
（Ⅱ）已知z=1+i，设z，z2，z-z2在复平面对应的点分别为A，B，C，求△ABC的面积．
已知复数z满足z（1-i）=3+i（其中i是虚数单位），则复数z的虚部为______．
已知复数z1，z2满足|z1|=|z2|=1，|z1-z2|=
3
，则|z1+z2|等于______．
设复数z1=1-i，z2=-1-xi（x∈R），若z1z2为纯虚数，则x的值是（　　）
A．-1B．-2C．1D．2
设复数z=
2i
1-i
，则
.
z
=（　　）
A．1+iB．1-iC．-1+iD．-1-i
已知复数z1=3+i，z2=1+2i，则复数
.
z1
=______，
z1
z2
=______．
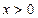设，若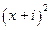是纯虚数（其中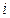为虚数单位），则          

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网