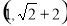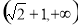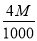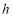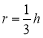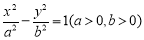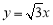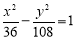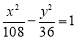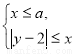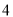题目内容
在平面直角坐标系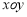 中,动点
中,动点 满足:点
满足:点 到定点
到定点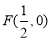 与到
与到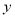 轴的距离之差为
轴的距离之差为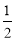 .记动点
.记动点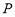 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线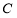 的轨迹方程;
的轨迹方程;
(2)过点 的直线交曲线
的直线交曲线 于
于 、
、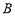 两点,过点
两点,过点 和原点
和原点 的直线交直线
的直线交直线 于点
于点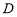 ,求证:直线
,求证:直线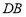 平行于
平行于 轴.
轴.
(1) ;(2)详见解析.
;(2)详见解析.
【解析】
试题分析:(1)由点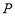 到定点
到定点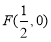 与到
与到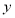 轴的距离之差为
轴的距离之差为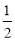 可得
可得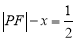 ,即
,即 ,化简可得轨迹方程为
,化简可得轨迹方程为 ;
;
(2)方法一:设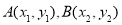 ,直线
,直线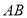 的方程为
的方程为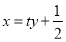 ,联立
,联立 得
得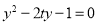
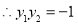 ,求出直线
,求出直线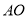 的方程为
的方程为
 点
点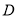 的坐标为
的坐标为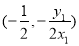 利用斜率可得
利用斜率可得 
 直线
直线 平行于
平行于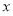 轴;
轴;
方法二:设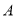 的坐标为
的坐标为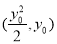 ,则
,则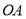 的方程为
的方程为
 点
点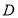 的纵坐标为
的纵坐标为 ,
,
 直线
直线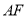 的方程为
的方程为
 点
点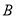 的纵坐标为
的纵坐标为 所以
所以 轴;当
轴;当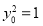 时,结论也成立,
时,结论也成立, 直线
直线 平行于
平行于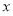 轴得证.
轴得证.
.
试题解析:(1)依题意: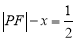 2分
2分
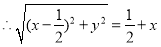
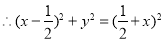 4分
4分
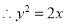 6分
6分
注:或直接用定义求解.
(2)设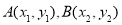 ,直线
,直线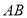 的方程为
的方程为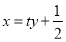
由 得
得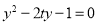 8分
8分
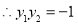
直线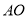 的方程为
的方程为
 点
点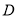 的坐标为
的坐标为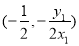 10分
10分
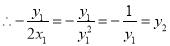
 直线
直线 平行于
平行于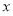 轴. 13分
轴. 13分
方法二:设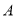 的坐标为
的坐标为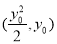 ,则
,则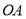 的方程为
的方程为
 点
点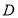 的纵坐标为
的纵坐标为 ,
,
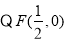
 直线
直线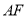 的方程为
的方程为
 点
点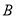 的纵坐标为
的纵坐标为 .
.
 轴;当
轴;当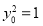 时,结论也成立,
时,结论也成立,
 直线
直线 平行于
平行于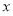 轴.
轴.
考点:1.直线与圆锥曲线的综合问题;2.轨迹方程;3.抛物线的标准方程.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
对具有线性相关关系的变量 ,
, 测得一组数据如下表:
测得一组数据如下表:
x | 2 | 4 | 5 | 6 | 8 |
y | 20 | 40 | 60 | 80 | 100 |
根据上表,利用最小二乘法得到它们的回归直线方程为 .据此模型预测
.据此模型预测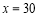 时,
时, 的估计值为( )
的估计值为( )
A. 320 B. 320.5 C. 322.5 D. 321.5