题目内容
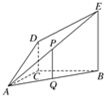 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE、AB的中点.
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE、AB的中点.(Ⅰ)证明:PQ∥平面ACD;
(Ⅱ)求异面直线AE与BC所成角的余弦值;
(Ⅲ)求AD与平面ABE所成角的正弦值.
分析:(Ⅰ)先利用P、Q分别是AE、AB的中点?PQ∥BE,PQ=
BE,再利用DC∥BE,DC=
BE可以推出PQ∥DC进而证明PQ∥平面ACD;
(Ⅱ)取BE的中点F,可以先推出QF∥AE且QF=
AE,所以∠DFQ就是异面直线AE与BC所成的角,然后在△DFQ中求出
∠DFQ的余弦值即可.
(Ⅲ)由AC=BC和Q为AB的中点可得CQ⊥AB,再利用DC⊥平面ABC,可得CQ⊥平面ABE,进而推出DP⊥平面ABE,所以∠DAP就是AD与平面ABE所成的角,在△DAP中求出∠DAP即可.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)取BE的中点F,可以先推出QF∥AE且QF=
| 1 |
| 2 |
∠DFQ的余弦值即可.
(Ⅲ)由AC=BC和Q为AB的中点可得CQ⊥AB,再利用DC⊥平面ABC,可得CQ⊥平面ABE,进而推出DP⊥平面ABE,所以∠DAP就是AD与平面ABE所成的角,在△DAP中求出∠DAP即可.
解答:解:(Ⅰ)证明:由已知:P、Q分别是AE、AB的中点,
所以,PQ∥BE,PQ=
BE,
又DC∥BE,DC=
BE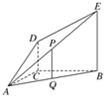
所以,PQ∥DC
所以,PQ∥平面ACD(4分)
(Ⅱ)取BE的中点F,连接QF,DF,DQ,可以推出QF∥AE且QF=
AE,
易证∠DFQ就是异面直线AE与BC所成的角
易知CQ=1,AB=2
,AE=4,QF=2,DF=BC=2,DQ=
由余弦定理:可得cos∠DFQ=
(8分)
(Ⅲ)由AC=BC和Q为AB的中点可得CQ⊥AB,
再利用DC⊥平面ABC,可得CQ⊥平面ABE,进而推出DP⊥平面ABE
所以∠DAP就是AD与平面ABE所成的角
DP=CQ=1,AD=
?sin∠DAP=
所以AD与平面ABE所成角的正弦值为
.(12分)
所以,PQ∥BE,PQ=
| 1 |
| 2 |
又DC∥BE,DC=
| 1 |
| 2 |

所以,PQ∥DC
所以,PQ∥平面ACD(4分)
(Ⅱ)取BE的中点F,连接QF,DF,DQ,可以推出QF∥AE且QF=
| 1 |
| 2 |
易证∠DFQ就是异面直线AE与BC所成的角
易知CQ=1,AB=2
| 3 |
| 2 |
由余弦定理:可得cos∠DFQ=
| 3 |
| 4 |
(Ⅲ)由AC=BC和Q为AB的中点可得CQ⊥AB,
再利用DC⊥平面ABC,可得CQ⊥平面ABE,进而推出DP⊥平面ABE
所以∠DAP就是AD与平面ABE所成的角
DP=CQ=1,AD=
| 5 |
| ||
| 5 |
所以AD与平面ABE所成角的正弦值为
| ||
| 5 |
点评:本题涉及了线面平行以及线线所成角和线面所成角,是对立体几何知识的综合考查.在证明线面平行时,其常用方法是在平面内找已知直线平行的直线.当然也可以用面面平行来推导线面平行.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
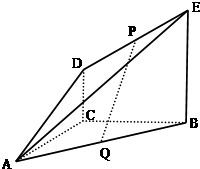 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=90°,P、Q分别为DE、AB的中点.
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=90°,P、Q分别为DE、AB的中点.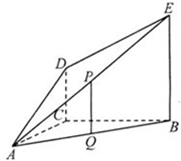 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.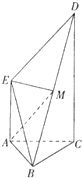 如图,DC⊥平面ABC,EA∥DC,AB=AC=AE=
如图,DC⊥平面ABC,EA∥DC,AB=AC=AE=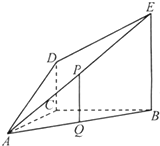 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.