题目内容
 如图,DC⊥平面ABC,EA∥DC,AB=AC=AE=
如图,DC⊥平面ABC,EA∥DC,AB=AC=AE=| 1 | 2 |
(Ⅰ)求证:EM∥平面ABC;
(Ⅱ)求证:平面AEM⊥平面BDC.
分析:(I)取BC的中点N,连接MN,AN,易证EANM是平行四边形,从而得EM∥AN,利用线面平行的判定定理即可证得EM∥平面ABC;
(II)依题意,易证EM⊥平面BDC,利用面面垂直的判定定理即可证得平面AEM⊥平面BDC.
(II)依题意,易证EM⊥平面BDC,利用面面垂直的判定定理即可证得平面AEM⊥平面BDC.
解答: 证明:(I)取BC的中点N,连接MN,AN,
证明:(I)取BC的中点N,连接MN,AN,
因为M为BD的中点,所以MN∥DC,且MN=
DC,
而EA∥DC且EA=
DC,
∴EA
MN,
∴EANM是平行四边形…2分
∴EM∥AN…3分
又因为EM?平面ABC,AN?平面ABC,
∴EM∥平面ABC,…5分
(II)
∵AB=AC,N为BC的中点,
∴AN⊥BC.
∵DC⊥平面ABC,AN?平面ABC,
∴DC⊥AN,
又DC∩BC=C,
∴AN⊥平面BDC,…7分
又AN∥EM,
∴EM⊥平面BDC,…9分
∵EM?平面AEM,
∴平面AEM⊥平面BDC…10分
 证明:(I)取BC的中点N,连接MN,AN,
证明:(I)取BC的中点N,连接MN,AN,因为M为BD的中点,所以MN∥DC,且MN=
| 1 |
| 2 |
而EA∥DC且EA=
| 1 |
| 2 |
∴EA
| ∥ |
. |
∴EANM是平行四边形…2分
∴EM∥AN…3分
又因为EM?平面ABC,AN?平面ABC,
∴EM∥平面ABC,…5分
(II)
∵AB=AC,N为BC的中点,
∴AN⊥BC.
∵DC⊥平面ABC,AN?平面ABC,
∴DC⊥AN,
又DC∩BC=C,
∴AN⊥平面BDC,…7分
又AN∥EM,
∴EM⊥平面BDC,…9分
∵EM?平面AEM,
∴平面AEM⊥平面BDC…10分
点评:本题考查平面与平面垂直的判定,考查直线与平面平行的判断,(Ⅰ)中证得EANM是平行四边形,(Ⅱ)中证得EM⊥平面BDC是关键,考查推理证明的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
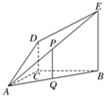 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE、AB的中点.
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE、AB的中点.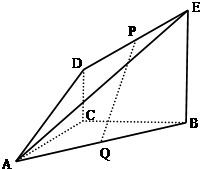 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=90°,P、Q分别为DE、AB的中点.
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=90°,P、Q分别为DE、AB的中点. 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.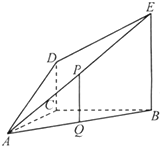 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.