题目内容
定义在(-1,1)上的函数f(x)满足:对任意x、y∈(-1,1)都有f(x)+f(y)=
![]() .
.
(1)求证:函数f(x)是奇函数;
(2)如果当x∈(-1,0)时,有f(x)>0,求证:f(x)在(-1,1)上是单调递减函数;
(3)在(2)的条件下解不等式:![]() +
+![]() >0.
>0.
答案:
解析:
解析:
答案:(1)证明:令x=y=0,则f(0)+f(0)=f(0),故f(0)=0. 令y=-x,则f(x)+f(-x)= ∴f(-x)=-f(x), 即函数f(x)是奇函数. (2)证明:设x1<x2∈(-1,1),则 f(x1)-f(x2)=f(x1)+f(-x2)= ∵x1<x2∈(-1,1), ∴x2-x1>0,-1<x1x2<1. 因此 ∴函数f(x)在(-1,1)上是减函数. (3)解:不等式 ∵函数f(x)在(-1,1)上是减函数, ∴ 解得: ∴原不等式的解集为{
|

练习册系列答案
相关题目
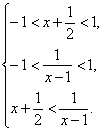
 ,
, ;
;