题目内容
如图,已知圆C1的方程为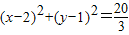 ,椭圆C2的方程为
,椭圆C2的方程为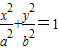 (a>b>0),C2的离心率为
(a>b>0),C2的离心率为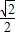 ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程.
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程.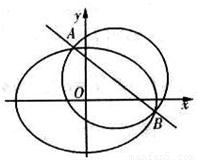
【答案】分析:由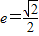 得,b2=c2,设椭圆方程为:
得,b2=c2,设椭圆方程为: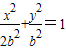 ,令A(x1,y1),B(x2,y2),由已知得圆心C1(2,1)为AB中点,A,B均在椭圆C2上,
,令A(x1,y1),B(x2,y2),由已知得圆心C1(2,1)为AB中点,A,B均在椭圆C2上,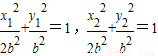 ,两式相减得:
,两式相减得: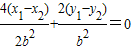 ,
,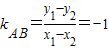 ,再由根的判别式结合题设条件可求出直线AB的方程和椭圆C2的方程.
,再由根的判别式结合题设条件可求出直线AB的方程和椭圆C2的方程.
解答:由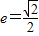 得
得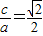 ,
,
∴a2=2c2,b2=c2,
设椭圆方程为: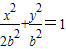 (2分)
(2分)
令A(x1,y1),B(x2,y2),
由已知得圆心C1(2,1)为AB中点,
∴x1+x2=4,y1+y2=2,
又A,B均在椭圆C2上,
∴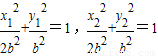 ,
,
两式相减得: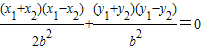
即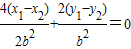
∴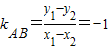 ,
,
即直线AB的方程为y-1=-(x-2)即x+y-3=0(6分)
将y=-x+3代入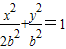 得3x2-12x+18-2b2=0(9分)
得3x2-12x+18-2b2=0(9分)
∴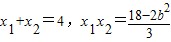 由直线AB与椭圆C2相交,
由直线AB与椭圆C2相交,
∴△=122-12(18-2b2)=24b2-72>0即b2>3,
又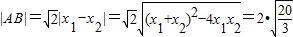 (11分)
(11分)
即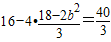 解得b2=8,故所求的椭圆方程为
解得b2=8,故所求的椭圆方程为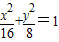 (13分)
(13分)
点评:本题考查直线和圆锥曲线的综合问题,解题时要认真审题,合理解答,注意公式的合理运用.
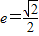 得,b2=c2,设椭圆方程为:
得,b2=c2,设椭圆方程为: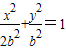 ,令A(x1,y1),B(x2,y2),由已知得圆心C1(2,1)为AB中点,A,B均在椭圆C2上,
,令A(x1,y1),B(x2,y2),由已知得圆心C1(2,1)为AB中点,A,B均在椭圆C2上,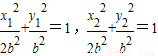 ,两式相减得:
,两式相减得: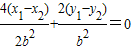 ,
,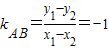 ,再由根的判别式结合题设条件可求出直线AB的方程和椭圆C2的方程.
,再由根的判别式结合题设条件可求出直线AB的方程和椭圆C2的方程.解答:由
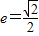 得
得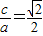 ,
,∴a2=2c2,b2=c2,
设椭圆方程为:
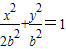 (2分)
(2分)令A(x1,y1),B(x2,y2),
由已知得圆心C1(2,1)为AB中点,
∴x1+x2=4,y1+y2=2,
又A,B均在椭圆C2上,
∴
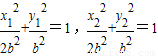 ,
,两式相减得:
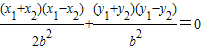
即
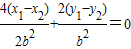
∴
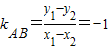 ,
,即直线AB的方程为y-1=-(x-2)即x+y-3=0(6分)
将y=-x+3代入
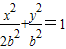 得3x2-12x+18-2b2=0(9分)
得3x2-12x+18-2b2=0(9分)∴
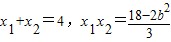 由直线AB与椭圆C2相交,
由直线AB与椭圆C2相交,∴△=122-12(18-2b2)=24b2-72>0即b2>3,
又
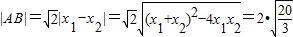 (11分)
(11分)即
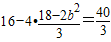 解得b2=8,故所求的椭圆方程为
解得b2=8,故所求的椭圆方程为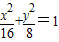 (13分)
(13分)点评:本题考查直线和圆锥曲线的综合问题,解题时要认真审题,合理解答,注意公式的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知圆C1的方程为
如图,已知圆C1的方程为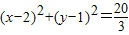 ,椭圆C2的方程为
,椭圆C2的方程为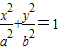 (a>b>0),C2的离心率为
(a>b>0),C2的离心率为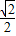 ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程.
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程.
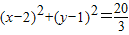 ,椭圆C2的方程为
,椭圆C2的方程为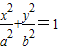 (a>b>0),C2的离心率为
(a>b>0),C2的离心率为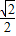 ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程.
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程.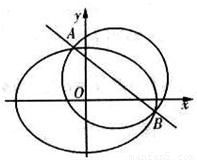
 ,椭圆C2的方程为
,椭圆C2的方程为 (a>b>0),C2的离心率为
(a>b>0),C2的离心率为 ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程.
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,求直线AB的方程和椭圆C2的方程.