题目内容
若
，
，且
，
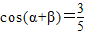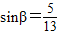，求（1）sin2β的值．
（2）cosα的值．
【答案】分析：（1）根据所给的角的范围和角的三角函数值，根据同角的三角函数的关系，写出要用的三角函数值，利用二倍角公式，代入数据得到结果．
（2）观察到角α是可以由角α+β减去β得到，根据两个角的差的余弦公式，代入数据，求出结果．
解答：解：∵若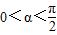
，
，
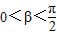∴0＜α+β＜π
，
，
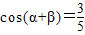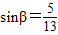∴sin（α+β）=
cosβ=
，
（1）sin2β=2sinβcosβ=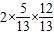
=
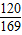
（2）cosα=cos[（α+β）-β]=cos（α+β）cosβ+sin（α+β）sinβ
=
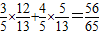
点评：本题考查角的变换和二倍角公式，本题解题的关键是根据所给的角的三角函数值和角的范围求出要用的函数值，本题是一个易错题．
（2）观察到角α是可以由角α+β减去β得到，根据两个角的差的余弦公式，代入数据，求出结果．
解答：解：∵若
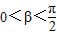，，∴0＜α+β＜π
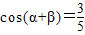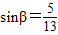，，∴sin（α+β）=
cosβ=
，（1）sin2β=2sinβcosβ=
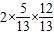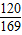
=（2）cosα=cos[（α+β）-β]=cos（α+β）cosβ+sin（α+β）sinβ
=
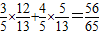
点评：本题考查角的变换和二倍角公式，本题解题的关键是根据所给的角的三角函数值和角的范围求出要用的函数值，本题是一个易错题．
练习册系列答案
阅读快车系列答案
相关题目
=-4，且
≤|AB|≤
，求直线l的斜率的取值范围．
=-4，且
≤|AB|≤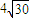
，求直线l的斜率的取值范围．